Superconducting Quantum Computing (SQC) Experiment

Quantum computing, namely the study of computing systems in which bits and gates are governed by the laws of quantum mechanics, is a topic that is currently attracting an enormous attention worldwide, with increasing efforts both on the financial and on the scientific side, especially in US, Japan and Europe. This is justified by the theoretical expectations: the introduction of quantum computing and processing tools would cause a revolution in many fields, from sciences to communications and economics. A quantum computer is not just a very fast computer: it is instead a tool of new kind, capable of achieving results out of reach for a classical computer, like the reduction fo exponentially complex problems to a polynomial complexity. As an example, let's think about the factorization of numbers with many digits, a feature that is at the base of current cryptography: a quantum computer could perform the task on a 1000 digits number in less than a second, whereas an ensable of classical workstations would take billions of years. Another important application is in performing efficient simulations of complex systems, like the behavior of organic macromolecules in the presence of viruses, which could open new scenarios to pharmaceutical research.
The physical implementation of a quantum bit must satisfy several conditions. The qubit is generally a two-state system, which can exist in a quantum superposition of the base states 0 and 1 and must persist in this state for a time long enough to allow the necessary operations (manipulation, preparation, readout). This condition requires that the decoherence induced on the system by the environment is reduced as much as possible, a characteristic that can vary very much from a physical implementation to the other.
For the practical implementation of quantum computing, the essential issues besides decoherence are scalability, integrability, possibility of individual addressing: these requirements lead naturally to a choice of solid-state devices, which however suffer from a more strict interaction with the environment (and hence shorter decoherence time) with respect to other systems, less scalable, like for instance trapped atoms. To manipulate these type of qubits, one generally uses NMR techniques, where oscillations between states are induced by microwave pulses.

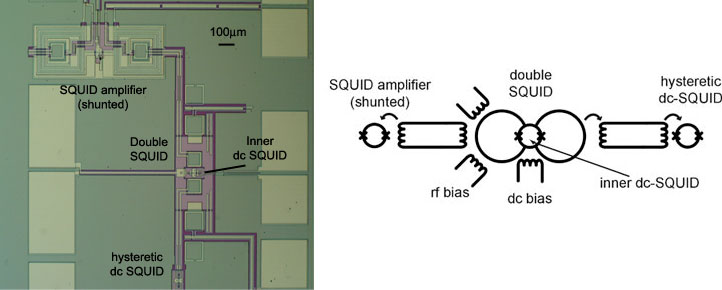
The solid-state qubits developed in SQC are superconducting qubits, based on the flux states of a superconducting quantum interferometer (SQUID). In the past years, the group developed an integrated system of SQUIDs, all built on a silicon chip with thin film and lithographic techniques. The junctions are made with Nb/AlOx/Nb trilayer technology. The figure below shows a microscope picture of the chip, showing the various devices: the double SQUID is the source of the qubit states, the readout is performed either by the dc-SQUID amplifier or by the readout hysteretic dc-SQUID; coupling and flux bias is achieved through superconducting transformers and coils.

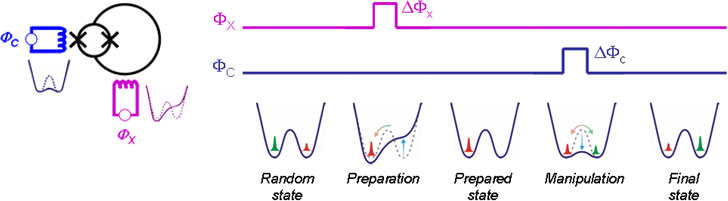
The basic device is the central double SQUID, that is a superconducting loop of inductance L interrupted by a small, two junction dc-SQUID (another smaller superconducting loop, with two Josephson junctions). The coordinate describing the system is the flux in the larger loop, while the inner dc-SQUID serves as a tunable Josephson junction.
For an appropriate choice of the constructive parameters, the potential presents two (or more) wells separated by barriers. At low temperature and for barriers high enough, one can consider a reduced Hilbert space with a base of only two flux states well localized in the minima. For fx=f0/2 the potential is symmetric, and coherent quantum oscillations between these flux states can occurs, with frequency exponentially dependent on the barrier height. This system can be used as a qubit by identifying the distinct flux states with the computational states “0” and “1”; these states can be prepared and manipulated by changing the potential balance (fx), and the readout can be performed by means of a flux magnetometer or a flux comparator.

The knobs to control the qubit are the magnetic fluxes coupled to the inner dc-SQUID, which has the purpose of changing the barrier height, and that coupled to the larger loop, which produces a tilting of the potential. Acting on these knobs, it is possible to prepare the qubit in a predetermined initial state and to forbid or to permit the coherent superposition.

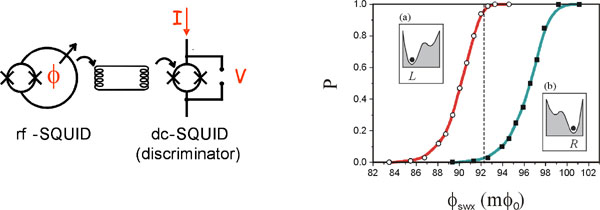
It is of extreme importance the use of a low disturbing readout device that can be rapidly turned on and off, giving the correct result with high fidelity. We have proposed, realized and characterized a sensitive, low disturbing flux comparator able to perform single shot, stroboscopic readout of an observed flux state. It is based on a small hysteretic dc-SQUID biased by short current pulses (below the device critical current), that exhibits transitions to the voltage state only if the applied flux is over a given critical threshold, depending on the working point, and that remains in the superconducting state otherwise. This device can be inductively linked to the rf-SQUID, and it is able to identify with high fidelity the relative flux state.

In order to manipulate the qubit, it is also possible to resort to microwave pulses, like in NMR techniques. In the first tests, we studied the effect of these pulses on the readout hysteretic dc-SQUID, showing that this device itself can act as a phase qubit. A first analysis of our results indicates the presence of population oscillations in the hysteretic dc SQUID. This result is very promising in view of using SQUIDs for more complex qubits systems.

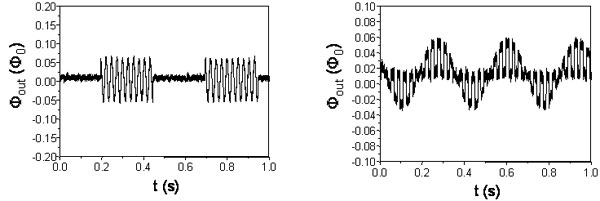
In order to operate on a real system, the coupling between qubits must be switchable. The figures below show how a switchable flux coupling can be implemented to connect two or more qubits.

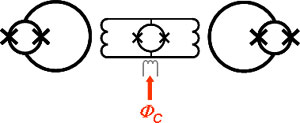
This can be achieved with a controlled flux coupling scheme (CFC) that we implemented by means of a superconducting transformer with a dc SQUID. We tested the device by sending sinusoidal signal at the input and recording the output, by means of a redout dc SQUID, in the on and off conditions. We achieved a on/off ratio of about 30.