|
| Contact |
|
Welcome |
|
|
 |
|
| Menu |
|
Research |
|
|
|
|
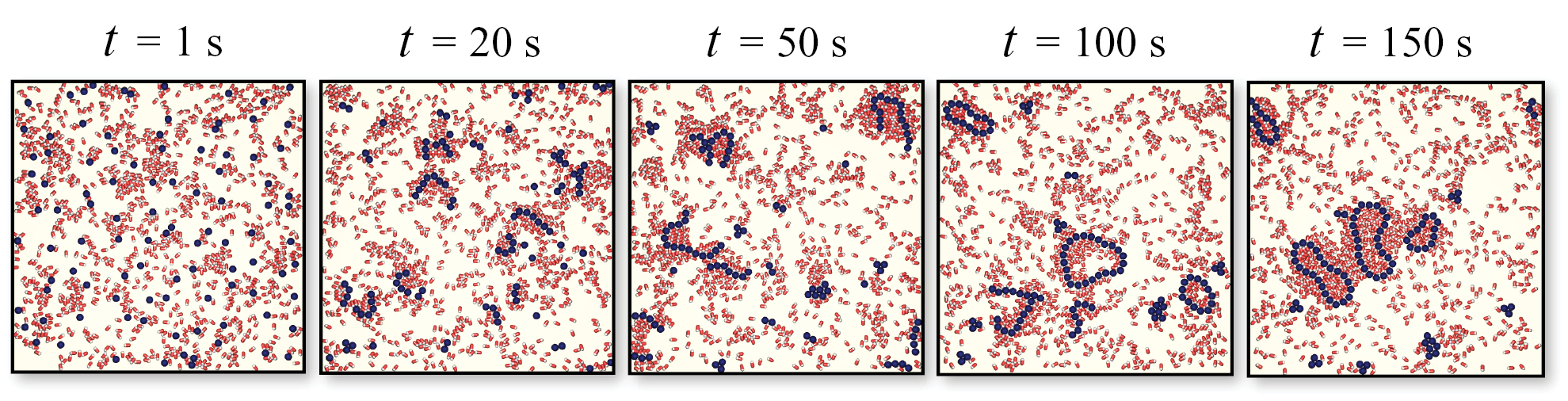
We explore the self-assembly process of colloidal structures immersed in active baths. By considering low-valence particles we numerically investigate the irreversible aggregation dynamics originated by the presence of run-and-tumble swimmers. We observe the formation of long closed chains—vesicles—densely filled by active swimmers. On the one hand the active bath drives the self-assembly of closed colloidal structures, and on the other hand the vesicles formation fosters the self-trapping of swimmers, suggesting new ways both to build structured nanomaterials and to trap microorganisms.
L. Angelani,
J. Phys.: Condens. Matter 31, 075101 (2019)
|
 |
|
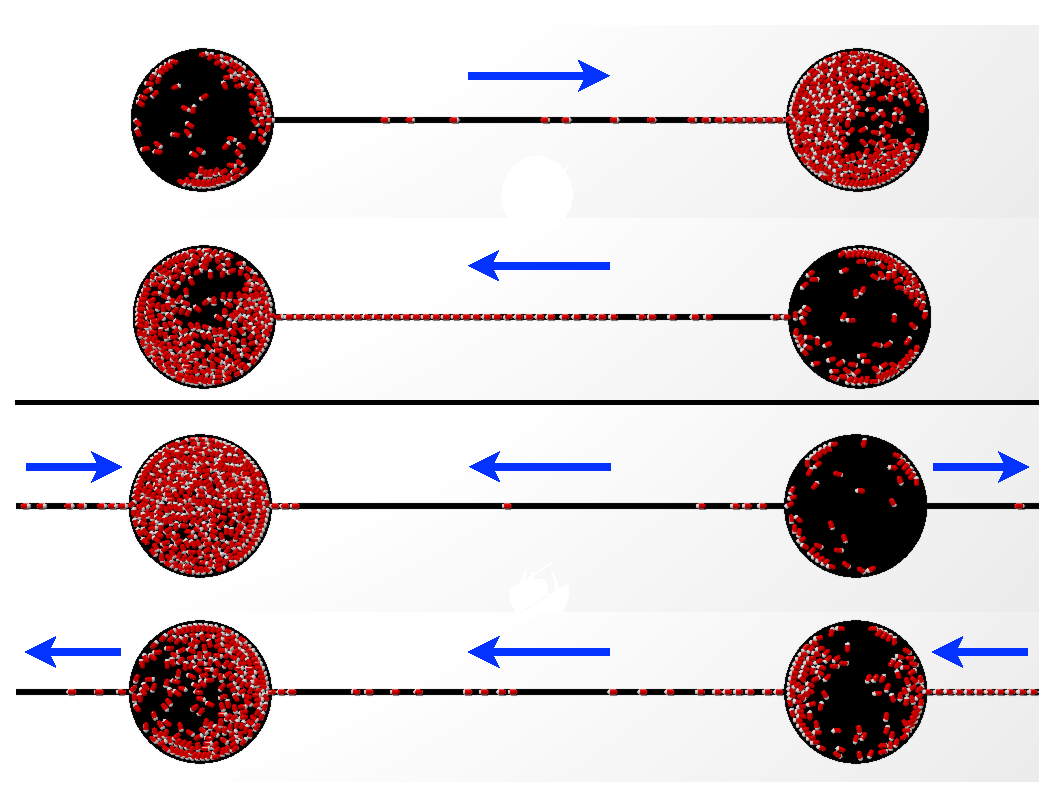
We numerically study the dynamics of run-and-tumble particles confined in two chambers connected by thin channels. Two dominant dynamical behaviors emerge: (i) an oscillatory pumping state, in which particles periodically fill the two vessels, and (ii) a circulating flow state, dynamically maintaining a near constant population level in the containers when connected by two channels. We demonstrate that the oscillatory behavior arises from the combination of a narrow channel, preventing bacteria reorientation, and a density-dependent motility inside the chambers.
M. Paoluzzi, R. Di Leonardo and L. Angelani,
Phys. Rev. Lett. 115, 188303 (2015)
Cover
of Physical Review Letters, 30 October 2015
|
 |
|
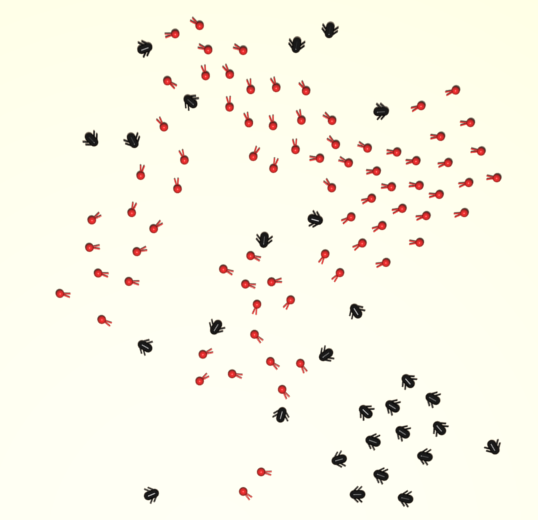
The phenomenon of collective predation is analyzed by using a simple individual-based model reproducing spatial animal movements. Two groups of self-propelled organisms are simulated by using Vicseklike models including steric intragroup repulsion. Chase and escape are described by intergroups interactions, attraction (for predators) or repulsion (for preys) from nearest particles of the opposite group. The quantitative analysis of some relevant quantities (total catch time, lifetime distribution, predation rate) allows us to characterize many aspects of the predation phenomenon and gives insights into the study of efficient escape strategies. The reported findings could be of relevance for many basic and applied disciplines, from statistical physics, to ecology, and robotics.
L. Angelani,
Phys. Rev. Lett. 109, 118104 (2012)
|
 |
 |
Protein folding of simplified off-lattice models
can be numerically analyzed
in terms of potential energy landscape properties.
By looking at stationary points (inherent structures, saddles)
sampled by the system,
a landscape characterization of the folding mechanism emerges.
|
|
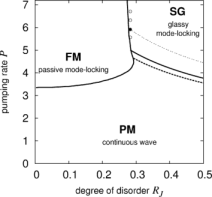
A random laser can be described as a statistical ensemble of interacting
objects (electromagnetic modes in an active non-linear random medium) through a disordered "spin-glass like" Hamiltonian.
Using standard statistical mechanics techniques of disordered systems,
it is possible to predict the existence of different phases:
continuous wave (paramagnetic), passive mode-locking (ferromagnetic)
and random mode-locking (glassy).
|
 |
 |
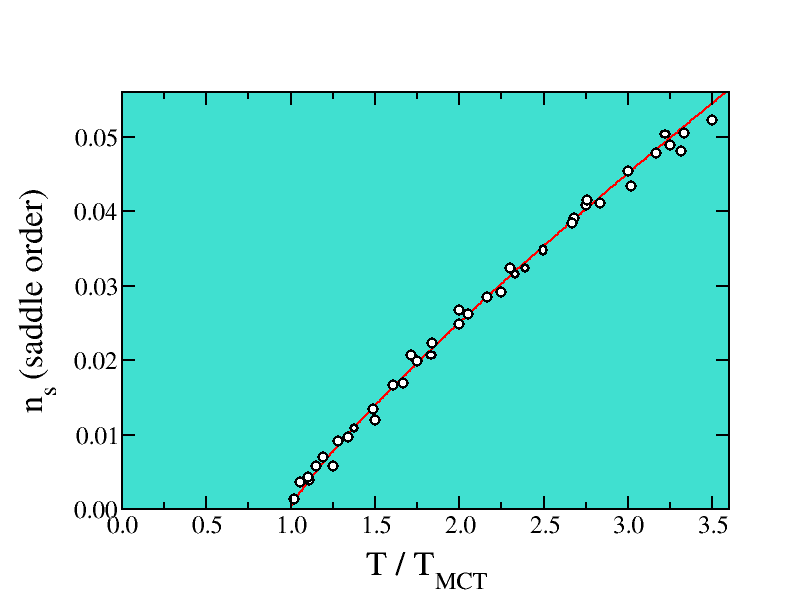The energy landscape characterization of the dynamical slowing-down in
supercooled liquids and glasses casts new light on the behaviour of
disordered systems.
|
|
Thermodynamic phase transitions can be associated to topological changes in the
potential energy landscape.
|
|
|
|
Generalized fluctuation relations are expected to describe the behaviour of
out-of-equilibrium systems. Numerical simulations help to verify such predictions
in model systems.
|
|
|
|
