



Next: Analisi nel baricentro
Up: Analisi grafica
Previous: Barre di incertezza
Indice
Nota la deviazione standard da attribuire
alle singole fluttuazioni delle 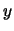 ,
si possono usare le
formule delle incertezza che si ricavano dal metodo dei
minimi quadrati, che qui riportiamo per comodità,
riscritte in termini delle grandezze che si conoscono e di quanto
altro sia facilmente valutabile per via grafica:
,
si possono usare le
formule delle incertezza che si ricavano dal metodo dei
minimi quadrati, che qui riportiamo per comodità,
riscritte in termini delle grandezze che si conoscono e di quanto
altro sia facilmente valutabile per via grafica:
Si noti che
Var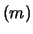 non è legata alle incertezze sulle
non è legata alle incertezze sulle 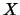 (convenzionalmente nulle): essa
misura invece la dispersione delle
(convenzionalmente nulle): essa
misura invece la dispersione delle  e
la sua radice quadrata è legata al
cosiddetto ``braccio di leva'' dei dati sperimentali.
È interessante notare come questo possa
essere valutato agevolmente dal grafico se i punti sono circa spaziati
lungo l'ascissa (caso tipico delle
esercitazioni di laboratorio). Approssimando
i punti sperimentali ad una distribuzione uniforme si
ottiene infatti12.2
Si faccia inoltre attenzione a non confondere il coefficiente
di correlazione fra i parametri (indicato con
e
la sua radice quadrata è legata al
cosiddetto ``braccio di leva'' dei dati sperimentali.
È interessante notare come questo possa
essere valutato agevolmente dal grafico se i punti sono circa spaziati
lungo l'ascissa (caso tipico delle
esercitazioni di laboratorio). Approssimando
i punti sperimentali ad una distribuzione uniforme si
ottiene infatti12.2
Si faccia inoltre attenzione a non confondere il coefficiente
di correlazione fra i parametri (indicato con 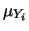 ) con
il coefficiente di correlazione fra ascisse e ordinate
dei punti sperimentali (indicato con
) con
il coefficiente di correlazione fra ascisse e ordinate
dei punti sperimentali (indicato con
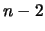 ): la grandezza di interesse
ai fini del risultato è
): la grandezza di interesse
ai fini del risultato è 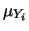 .
.




Next: Analisi nel baricentro
Up: Analisi grafica
Previous: Barre di incertezza
Indice
Giulio D'Agostini
2001-04-02