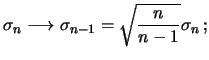 :
:
La misura più precisa, ovvero quella che ha il più basso errore percentuale, è la prima.
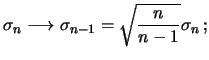 :
:
Se si suppone che la deviazione standard della singola pesata sia la stessa per le tre misure, la migliore stima di essa è ottenuta dal campione di 15 misurazioni ( in realtà si può anche combinare l'informazione del campione di tre misurazioni, pesando le due varianza con il numero di gradi di libertà, ma l'influenza è minima ):
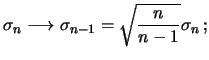 :
:
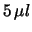 C.L.:
C.L.:
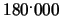 ;
;
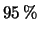 C.L.:
C.L.:
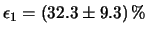 .
.
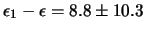 persone: praticamente impossibile.
persone: praticamente impossibile.
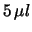 C.L.:
C.L.:
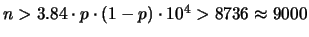 ;
;
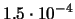 al
al 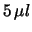 C.L.. Quale
dei due farmaci è migliore?
C.L.. Quale
dei due farmaci è migliore?
Per ottenere risultati del genere bisogna avere piante omozigote con purezze del
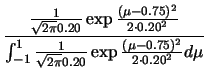 .
.
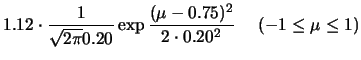 |
|||
b)
-
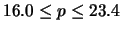 ;
;
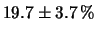 ,
da cui, al
,
da cui, al 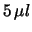 C.L.:
C.L.:
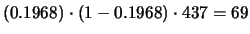 ,
oppure
,
oppure
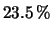 .
.
- ricaviamoci di nuovo la soluzione attaverso il seguente ragionamento:
dal valore di percentuale riportato dal giornale si ricava che il
numero di persone che ha dichiarato di votare per il partito A
è 86. Questo numero rappresenta la migliore stima del
valore aspettato della variabile, da cui segue che la
migliore stima di
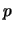 è 0.1968
( stiamo andando a ritroso ).
La migliore stima della varianza della variabile casuale
è
è 0.1968
( stiamo andando a ritroso ).
La migliore stima della varianza della variabile casuale
è
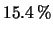 . Otteniamo quindi
8.3 come migliore stima della sua deviazione standard e quindi
la migliore stima della deviazione standard di
. Otteniamo quindi
8.3 come migliore stima della sua deviazione standard e quindi
la migliore stima della deviazione standard di 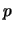 è
8.3/437=0.019.
è
8.3/437=0.019.
- Come mai in questo caso, nel calcolo dell'intervallo di
fiducia, non c'è bisogno di dividere per
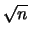 ?
?
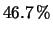 ( e non
( e non 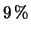 ! ).
! ).
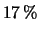 .
.
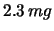 .
.
- Ovviamente la probabilità non è intorno al
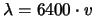 , ma molto
più grande.
Vedi anche i problemi 20 e 25 (*** attenzione alla numerazione ***).
, ma molto
più grande.
Vedi anche i problemi 20 e 25 (*** attenzione alla numerazione ***).
 .
.
- Una sola misura da 6400 secondi:
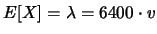 .
.
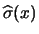

![$\displaystyle E[X] = \lambda = 6400\cdot v$](img2280.png)
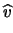

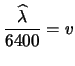
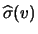

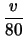
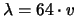

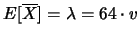
- 100 misure da 64 secondi
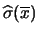 :
:
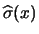

![$\displaystyle E[\overline{X}] = \lambda = 64\cdot v$](img2288.png)
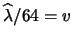

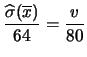
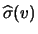

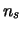
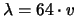

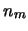
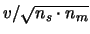 il numero di secondi
della misura e
il numero di secondi
della misura e  il numero di misure l'incertezza
atteso sulla grandezza
fisica è sempre
il numero di misure l'incertezza
atteso sulla grandezza
fisica è sempre
 .
Ovviamente il secondo metodo permette di controllare se ci sono
eventuali derive con il tempo del valore vero ed è da preferire se
lo sperimentatore
è in grado di sobbarcarsi i costi aggiuntivi - in senso lato -
che il registrare molte misure comporta.
.
Ovviamente il secondo metodo permette di controllare se ci sono
eventuali derive con il tempo del valore vero ed è da preferire se
lo sperimentatore
è in grado di sobbarcarsi i costi aggiuntivi - in senso lato -
che il registrare molte misure comporta.
- Una sola misura da 6400 secondi: