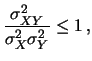Next: Matrice di covarianza e
Up: Covarianza e coefficiente di
Previous: Variabili correlate e misura
Indice
Proprietà formali di covarianza e coefficiente
di correlazione
Avendo introdotto il concetto di covarianza, vediamo il modo con cui
essa viene calcolata a partire dalla definizione.
Il secondo passaggio, fra parentesi, mostra il modo di calcolare
la covarianza dalla definizione operativa (avendo preso
come esempio
il caso di variabili continue). In realtà la
(9.19) rappresenta il modo più semplice
per calcolare la covarianza, in analogia alla formula che esprime
la varianza come ``media dei quadrati meno il quadrato della media''.
Infatti, anche la (9.19) può essere
letta come ``media del prodotto meno il prodotto delle medie''.
Per quanto riguarda
E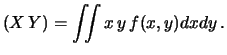 , esso non è in genere
risolvibile in termine di altre grandezze note e va calcolato dalla
definizione operativa, che, per variabili continue, è
, esso non è in genere
risolvibile in termine di altre grandezze note e va calcolato dalla
definizione operativa, che, per variabili continue, è
E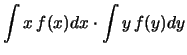 |
(9.20) |
Esiste un solo caso notevole in cui è possibile evitare di
fare l'integrale doppio. Se
ovvero  e
e 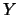 sono fra loro indipendenti, possiano
riscrivere l'integrale doppio come prodotto di due integrali:
sono fra loro indipendenti, possiano
riscrivere l'integrale doppio come prodotto di due integrali:
Ne segue, allora, che
Cov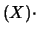 E
E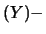 E
E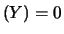 E
E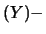 E
E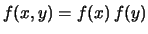 :
:
se due variabili casuali sono indipendenti, la loro covarianza
è nulla.
Si faccia attenzione a questa affermazione. Essa si basa sulla
definizione di indipendenza stocastica espressa
dalla
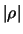 e non significa che non esista
alcun legame fra i possibili valori delle due variabili.
La covarianza nulla
implica soltanto l'assenza
di una correlazione di tipo lineare, come
si vedrà fra breve quando vedremo i casi che massimizzano
e non significa che non esista
alcun legame fra i possibili valori delle due variabili.
La covarianza nulla
implica soltanto l'assenza
di una correlazione di tipo lineare, come
si vedrà fra breve quando vedremo i casi che massimizzano 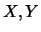 .
Due variabili
possono essere fortemente dipendenti pur avendo covarianza nulla.
Un caso ``clamoroso'' è quello di punti nel piano
.
Due variabili
possono essere fortemente dipendenti pur avendo covarianza nulla.
Un caso ``clamoroso'' è quello di punti nel piano 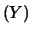 distribuiti lungo una circonferenza. Se per semplicità poniamo
il centro del cerchio nell'origine è facile verificare che
sono nulli
E
distribuiti lungo una circonferenza. Se per semplicità poniamo
il centro del cerchio nell'origine è facile verificare che
sono nulli
E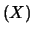 ,
E
,
E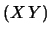 e
E
e
E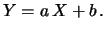 e quindi anche la covarianza (vedi figura 9.2).
e quindi anche la covarianza (vedi figura 9.2).
Calcoliamo ora covarianza e coefficiente di correlazione
fra due variabili linearmente dipendenti,
ovvero legate da una relazione del tipo
Utilizzando i simboli compatti
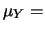 E
E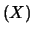 e
e
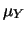 E
E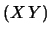 , abbiamo:
, abbiamo:
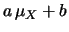 |
 |
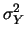 |
(9.22) |
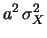 |
 |
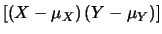 |
(9.23) |
Cov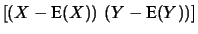 |
 |
E![$\displaystyle [(X-\mu_X)\, (Y-\mu_Y)]$](img2284.png) |
|
| |
 |
E![$\displaystyle [(X-\mu_X)\, (a\, X+b-a\, \mu_X-b)]$](img2285.png) |
|
| |
 |
E![$\displaystyle [a\, (X-\mu_X)\, (X-\mu_X)]$](img2286.png) |
|
| |
 |
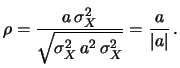 |
(9.24) |
da cui
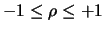 |
(9.25) |
Quindi, in caso di dipendenza lineare,
il coefficiente di correlazione vale  a seconda che
il coefficiente angolare
a seconda che
il coefficiente angolare 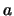 sia positivo o negativo.
Si può dimostrare che, in generale,
sia positivo o negativo.
Si può dimostrare che, in generale,
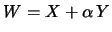 |
(9.26) |
e il grado di correlazione lineare fra due variabili è misurato da 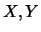 .
.
Dimostrazione della (9.26): consideriamo la variabile
casuale
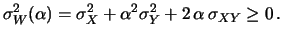 .
La varianza
di
.
La varianza
di 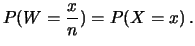 è, per definizione, non negativa per qualsiasi valore di
è, per definizione, non negativa per qualsiasi valore di 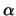 :
:
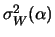 |
(9.27) |
La dipendenza di
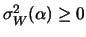 da
da 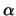 è parabolico.
Essendo
è parabolico.
Essendo
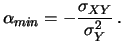 ,
questo sarà vero anche
quando
,
questo sarà vero anche
quando
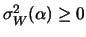 assume il valore minimo,
in corrispondenza di
Sostituendo nella (9.27) si ottiene
assume il valore minimo,
in corrispondenza di
Sostituendo nella (9.27) si ottiene
 |
(9.28) |
da cui segue la (9.26).
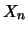




Next: Matrice di covarianza e
Up: Covarianza e coefficiente di
Previous: Variabili correlate e misura
Indice
Giulio D'Agostini
2001-04-02
![$\displaystyle \left[\left(X-\mbox{E}(X)\right)\,
\left(Y-\mbox{E}(Y)\right)\right]$](img2259.png)
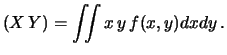 , esso non è in genere
risolvibile in termine di altre grandezze note e va calcolato dalla
definizione operativa, che, per variabili continue, è
, esso non è in genere
risolvibile in termine di altre grandezze note e va calcolato dalla
definizione operativa, che, per variabili continue, è
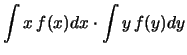
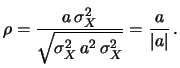
![]() .
La varianza
di
.
La varianza
di ![]() è, per definizione, non negativa per qualsiasi valore di
è, per definizione, non negativa per qualsiasi valore di ![]() :
: