



Next: Problemi
Up: Impostazione del problema. Caso
Previous: Distribuzione predittiva
Indice
Combinazione scettica
Nel paragrafo 11.3 abbiamo visto come
combinare risultati parziali indipendenti in un risultato globale.
Consideriamo ora il caso illustrato in figura 11.11
in cui le masse di probabilità indicate da ciascuna inferenza
(curve puntinate)
Figura:
Esempio di combinazione di risultati parziali
in ``palese'' (vedi testo) disaccordo fra di loro. La curva
continua rappresenta l'inferenza globale ottenuta dalla ``formula
standard'' di combinazione. Quella tratteggiata tiene conto del
forte dubbio che ci sia qualche effetto spurio fra i diversi risultati.
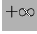 |
non si sovrappongono11.9. Applicando le formule di combinazione
(11.12) e ((11.13) si ottiene
il risultato indicato con la curva continua di figura 11.11.
A questo punto ci sono ottime ragioni per rimanere perplessi:
il risultato finale concentra la probabilità in una zona
molto più ristretta del singolo risultato parziale, ma non indicata da
nessuno di quei risultati, non tenendo conto dell'enorme variabilità
da un risultato all'altro. Cerchiamo di capire cosa sta succedendo,
elencando le ipotesi alla base della ``combinazione standard'' data
dalle (11.12) e ((11.13).
- Tutte le misure si riferiscono alla stessa grandezza (``stiamo misurando
tutti la stessa cosa'').
- La verosimiglianza di ciascuna misura è descritta da una gaussiana.
- Il parametro
 della gaussiana è stato stimato correttamente.
della gaussiana è stato stimato correttamente.
- I risultati sono indipendenti.
- Infine, la conoscenza iniziale di
 è supposta essere sufficientemente
vaga rispetto a quanto forniscono le singole
verosimiglianze.
è supposta essere sufficientemente
vaga rispetto a quanto forniscono le singole
verosimiglianze.
Se crediamo in modo assoluto a tutte queste ipotesi, non possiamo far
altro che accettare il risultato ottenuto dalla combinazione standard,
in quanto, trattandosi di fenomeni aleatori, l'osservazione di
questa configurazione di risultati parziali non è incompatibile con
con il modello (come non è incompatibile con le leggi della probabilità
che una moneta dia testa 100 volte di seguito, o che un processo poissoniano
di 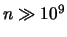 produca l'osservazione
produca l'osservazione 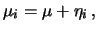 . Nonostante questi richiami
alle ``leggi del caso'', qualsiasi persona esperta è disposta a scommettere
che c'e' qualcosa che non va nei quattro risultati di figura
11.11. E ha ragione. Il motivo è che
un ricercatore esperto ha sviluppato delle
fortissime prior11.10 sul
comportamento di strumentazioni, misure ...e colleghi.
Sulla base di queste prior, sa che gli strumenti
possono essere non calibrati, che le tecniche sperimentali possono
essere inadeguate allo misura particolare, che i colleghi si possono
sbagliare, e così via. Alla luce di queste considerazioni, è
praticamente sicuro che che qualcosa sia andata male nelle
misure, piuttosto che attribuire la dispersione di risultati
al puro caso.
. Nonostante questi richiami
alle ``leggi del caso'', qualsiasi persona esperta è disposta a scommettere
che c'e' qualcosa che non va nei quattro risultati di figura
11.11. E ha ragione. Il motivo è che
un ricercatore esperto ha sviluppato delle
fortissime prior11.10 sul
comportamento di strumentazioni, misure ...e colleghi.
Sulla base di queste prior, sa che gli strumenti
possono essere non calibrati, che le tecniche sperimentali possono
essere inadeguate allo misura particolare, che i colleghi si possono
sbagliare, e così via. Alla luce di queste considerazioni, è
praticamente sicuro che che qualcosa sia andata male nelle
misure, piuttosto che attribuire la dispersione di risultati
al puro caso.
Dopo queste riflessioni, si tratta di rimodellizzare il problema,
cercando di modificare una o più delle ipotesi alla base
della combinazione normale. Come si capisce, il problema non ha
una soluzione unica. Si tratta soltanto di scegliere i modelli che
sembrano più ragionevoli e confrontarne i risultati. La sola ipotesi
tranquilla è quella sulla prior uniforme su  .
In questo testo non intendiamo affrontare il caso più
generale11.11,
ma ci limitiamo a fornire delle indicazioni su caso illustrato
nella figura 11.11 di risultati ``molto incompatibili''
fra di loro. Ciascuna delle ipotesi 1-3 possono essere soggette a critica.
Un modo di schematizzare il problema è quello di concentrarsi sulla 1
e 3. Il ricercatore esperto dirà infatti che ``non stiamo misurando
la stessa cosa'', ovvero ``ci siamo dimenticati di effetti sistematici,
diversi in entità in ciascun risultato parziale'' (il che
è più o meno la stessa cosa), ovvero punta il dito sull'ipotesi 1:
.
In questo testo non intendiamo affrontare il caso più
generale11.11,
ma ci limitiamo a fornire delle indicazioni su caso illustrato
nella figura 11.11 di risultati ``molto incompatibili''
fra di loro. Ciascuna delle ipotesi 1-3 possono essere soggette a critica.
Un modo di schematizzare il problema è quello di concentrarsi sulla 1
e 3. Il ricercatore esperto dirà infatti che ``non stiamo misurando
la stessa cosa'', ovvero ``ci siamo dimenticati di effetti sistematici,
diversi in entità in ciascun risultato parziale'' (il che
è più o meno la stessa cosa), ovvero punta il dito sull'ipotesi 1:
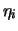 |
(11.107) |
avendo indicato con  il valore ideale che tutti ``volevano misurare'',
il valore ideale che tutti ``volevano misurare'',
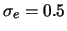 l'errore sistematico di entità ignota, e
l'errore sistematico di entità ignota, e 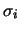 il valore
vero che essi ``hanno in fatti determinato''.
il valore
vero che essi ``hanno in fatti determinato''.
Se sapessimo, mediante opportune calibrazioni, quanto vale 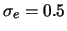 per ciascun laboratorio, il nostro problema
è risolto. Ma se siamo in questa situazione è perché non
non riusciamo a intercalibrare i laboratori e, inoltre, non abbiamo alcun
motivo di preferire uno di essi. A questo punto non possiamo
fare altro che considerare
per ciascun laboratorio, il nostro problema
è risolto. Ma se siamo in questa situazione è perché non
non riusciamo a intercalibrare i laboratori e, inoltre, non abbiamo alcun
motivo di preferire uno di essi. A questo punto non possiamo
fare altro che considerare 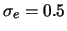 come un errore aleatorio e stimarne
la distribuzione dalla dispersione dei dati sperimentali, come
abbiamo visto nei paragrafi precedenti, ritenendo il modello
gaussiano per semplicità. Il caso numeri co in esame si presta
particolarmente bene per quasta modellizzazione, in quanto possiamo
ignorare completamente le singole deviazioni standard e concentrarci soltanto
sui valori centrali. Il risultato è di **** ed è mostrato
nella curva tratteggiata. Come si vede, tale curva descrive abbastanza
bene la nostra incertezza, in quanto il valore vero si può trovare
con alta probabilità fra il risultato minimo e quello massimo.
come un errore aleatorio e stimarne
la distribuzione dalla dispersione dei dati sperimentali, come
abbiamo visto nei paragrafi precedenti, ritenendo il modello
gaussiano per semplicità. Il caso numeri co in esame si presta
particolarmente bene per quasta modellizzazione, in quanto possiamo
ignorare completamente le singole deviazioni standard e concentrarci soltanto
sui valori centrali. Il risultato è di **** ed è mostrato
nella curva tratteggiata. Come si vede, tale curva descrive abbastanza
bene la nostra incertezza, in quanto il valore vero si può trovare
con alta probabilità fra il risultato minimo e quello massimo.
Discutere in footnote il caso intermedio: vedi mail a Press.




Next: Problemi
Up: Impostazione del problema. Caso
Previous: Distribuzione predittiva
Indice
Giulio D'Agostini
2001-04-02
![]() .
In questo testo non intendiamo affrontare il caso più
generale11.11,
ma ci limitiamo a fornire delle indicazioni su caso illustrato
nella figura 11.11 di risultati ``molto incompatibili''
fra di loro. Ciascuna delle ipotesi 1-3 possono essere soggette a critica.
Un modo di schematizzare il problema è quello di concentrarsi sulla 1
e 3. Il ricercatore esperto dirà infatti che ``non stiamo misurando
la stessa cosa'', ovvero ``ci siamo dimenticati di effetti sistematici,
diversi in entità in ciascun risultato parziale'' (il che
è più o meno la stessa cosa), ovvero punta il dito sull'ipotesi 1:
.
In questo testo non intendiamo affrontare il caso più
generale11.11,
ma ci limitiamo a fornire delle indicazioni su caso illustrato
nella figura 11.11 di risultati ``molto incompatibili''
fra di loro. Ciascuna delle ipotesi 1-3 possono essere soggette a critica.
Un modo di schematizzare il problema è quello di concentrarsi sulla 1
e 3. Il ricercatore esperto dirà infatti che ``non stiamo misurando
la stessa cosa'', ovvero ``ci siamo dimenticati di effetti sistematici,
diversi in entità in ciascun risultato parziale'' (il che
è più o meno la stessa cosa), ovvero punta il dito sull'ipotesi 1:
![]() per ciascun laboratorio, il nostro problema
è risolto. Ma se siamo in questa situazione è perché non
non riusciamo a intercalibrare i laboratori e, inoltre, non abbiamo alcun
motivo di preferire uno di essi. A questo punto non possiamo
fare altro che considerare
per ciascun laboratorio, il nostro problema
è risolto. Ma se siamo in questa situazione è perché non
non riusciamo a intercalibrare i laboratori e, inoltre, non abbiamo alcun
motivo di preferire uno di essi. A questo punto non possiamo
fare altro che considerare ![]() come un errore aleatorio e stimarne
la distribuzione dalla dispersione dei dati sperimentali, come
abbiamo visto nei paragrafi precedenti, ritenendo il modello
gaussiano per semplicità. Il caso numeri co in esame si presta
particolarmente bene per quasta modellizzazione, in quanto possiamo
ignorare completamente le singole deviazioni standard e concentrarci soltanto
sui valori centrali. Il risultato è di **** ed è mostrato
nella curva tratteggiata. Come si vede, tale curva descrive abbastanza
bene la nostra incertezza, in quanto il valore vero si può trovare
con alta probabilità fra il risultato minimo e quello massimo.
come un errore aleatorio e stimarne
la distribuzione dalla dispersione dei dati sperimentali, come
abbiamo visto nei paragrafi precedenti, ritenendo il modello
gaussiano per semplicità. Il caso numeri co in esame si presta
particolarmente bene per quasta modellizzazione, in quanto possiamo
ignorare completamente le singole deviazioni standard e concentrarci soltanto
sui valori centrali. Il risultato è di **** ed è mostrato
nella curva tratteggiata. Come si vede, tale curva descrive abbastanza
bene la nostra incertezza, in quanto il valore vero si può trovare
con alta probabilità fra il risultato minimo e quello massimo.