



Next: Probabilità delle cause e
Up: Regole della probabilità
Previous: Ricapitolando
Indice
- Dati i eventi
 ,
,  e
e 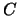 , scrivere l'espressione dei seguenti eventi:
, scrivere l'espressione dei seguenti eventi:
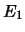 = ``si verifica soltanto
= ``si verifica soltanto  '';
'';
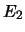 = ``si verificano sia
= ``si verificano sia  che
che  che
che 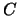 '';
'';
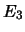 = ``non si verifica né
= ``non si verifica né  , né
, né  , né
, né 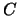 '';
'';
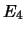 = ``si verifica almeno uno degli eventi'';
= ``si verifica almeno uno degli eventi'';
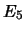 = ``si verificano al più due eventi'';
= ``si verificano al più due eventi'';
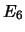 = ``si verificano
= ``si verificano  e
e  , indipendentemente dall'esito di
, indipendentemente dall'esito di 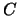 '';
'';
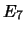 = ``si verifica
= ``si verifica  indipendentemente dall'esito degli altri'';
indipendentemente dall'esito degli altri'';
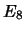 = ``si verifica
= ``si verifica  , ma non
, ma non  , indipendentemente dall'esito
di
, indipendentemente dall'esito
di 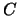 '';
'';
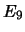 = ``si verificano tutti o (``OR'') nessuno degli eventi''
= ``si verificano tutti o (``OR'') nessuno degli eventi''
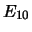 = ``si verifica
= ``si verifica  indipendentemente dagli altri due,
o (``OR'') si verifica
uno degli altri due''
indipendentemente dagli altri due,
o (``OR'') si verifica
uno degli altri due''
- Consideriamo i seguenti eventi:
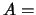 ``una macchina è
della marca X'';
``una macchina è
della marca X''; 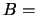 ``una macchina è bianca''.
Sapendo che le probabilità di
``una macchina è bianca''.
Sapendo che le probabilità di  vale 1/3, la probabilità
di
vale 1/3, la probabilità
di  vale 1/2 e che il
vale 1/2 e che il 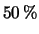 delle macchine X sono
bianche:
delle macchine X sono
bianche:
- calcolare le probabilità dei seguenti eventi:
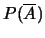 ;
;
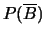 ;
;
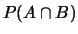 ;
;
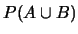 ;
;
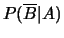 ;
;
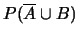 ;
;
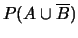 ;
;
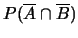 ;
;
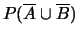 ;
;
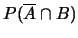 ;
;
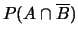 ;
;
- esprimere a parole gli eventi di cui è richiesto
il calcolo della probabilità al punto a);
- supponendo che il numero di macchine sia talmente
elevato per cui la probabilità di osservare un certo tipo di
macchina non sia influenzato dall'osservazione precedente,
calcolare: la probabilità di osservare due volte consecutive
una macchina bianca; la probabilità che dopo una macchina
X segua una macchina non bianca;
- Una persona crede che
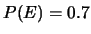 e
e
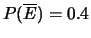 .
È possibile tale assegnazione di probabilità?
Si immagini che, con tale convinzione,
egli faccia due scommesse legate a tale evento
nelle quali
punta 7000 lire per ricevere 10000 se l'evento si verifica
e punta 4000 lire per ricevere 10000 se l'evento non si verifica.
Fareste mai simili scommesse?
.
È possibile tale assegnazione di probabilità?
Si immagini che, con tale convinzione,
egli faccia due scommesse legate a tale evento
nelle quali
punta 7000 lire per ricevere 10000 se l'evento si verifica
e punta 4000 lire per ricevere 10000 se l'evento non si verifica.
Fareste mai simili scommesse?
- Un allibratore improvvisato ritiene che
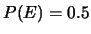 e
e
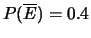 . Pertanto accetta una scommessa
di 5000 per pagarne 10000 se l'evento si verifica, e contemporaneamente
una scommessa di 4000 per pagarne 10000 se l'evento non si verifica.
Sta facendo un buon affare?
. Pertanto accetta una scommessa
di 5000 per pagarne 10000 se l'evento si verifica, e contemporaneamente
una scommessa di 4000 per pagarne 10000 se l'evento non si verifica.
Sta facendo un buon affare?
- Consideriamo due eventi arbitrari
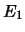 e
e 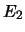 .
Una persona attribuisce ad essi
.
Una persona attribuisce ad essi
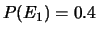 ,
,
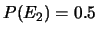 e
e
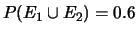 . Le valutazioni sono coerenti?
. Le valutazioni sono coerenti?
- Una persona ritiene che
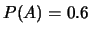 ,
, 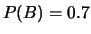 . È possibile?
Quanto deve essere il valore minimo
della probabilità del prodotto logico dei due eventi?
. È possibile?
Quanto deve essere il valore minimo
della probabilità del prodotto logico dei due eventi?
- Quanto vale la probabilità che, estraendo da un mazzo di carte italiane
una carta, questa sia una coppe o una figura?
- Definiti gli eventi
 e
e  , una persona valuta
, una persona valuta
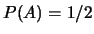 ,
, 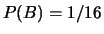 e
e
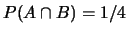 . Verificare se
l'assegnazione delle
probabilità è coerente.
. Verificare se
l'assegnazione delle
probabilità è coerente.
- Una persona si dichiara convinta che una squadra di calcio
ha una probabilità dell' 80% di passare
in vantaggio al primo tempo
e di vincere poi l'incontro. Successivamente
afferma che la probabilità che la squadra passi in vantaggio
al primo tempo è del 50%? Sono coerenti le sue affermazioni?
- Un'urna contiene 4 palline nere e 3 rosse. Si estraggono
a caso 3 palline senza rimetterle nell'urna. Quanto vale
la probabilità che rispettivamente
nessuna, una, due e tre palline siano rosse?
- Rispondere alle stesse domande dell'esercizio precedente
nel caso che le palline vengano reintrodotte nell'urna.
- Un'urna contiene una pallina bianca, una rossa e una nera.
Una seconda urna ne contiene una bianca, una rossa, una nera e
una gialla. Si estrare una pallina da ciascuna delle urne. Identifichiamo
l'eventi con l'iniziale del colore e un indice che vale
1 o due a seconda dell'urna. Determinare la probabilità
dei seguenti eventi:
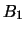 ;
;
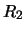 ;
;
-
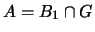 ;
;
-
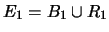 ;
;
-
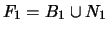
-
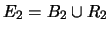 ;
;
-
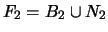 ;
;
-
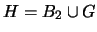 .
.
Verificare inoltre se sono fra di loro indipendenti:
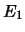 e
e 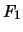 ;
;
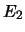 e
e 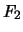 ;
;
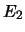 e
e 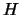 ;
;
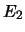 ,
, 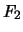 e
e 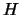 .
.
- Roulette russa: ogni giocatore
ruota a caso il tamburo di una pistola e poi si spara.
Qual'è la probabilità di sopravvivere dopo
 prove, se
ogni volta si fa
ruotare il tamburo? (La pistola ha sei colpi)
prove, se
ogni volta si fa
ruotare il tamburo? (La pistola ha sei colpi)
- Variante (col morto) della roulette russa.
Sei giocatori decidono di ruotare a caso una sola volta il tamburo
e di provare uno dopo l'altro. Quale dei giocatori ha
maggiore probabilità di sopravvivere?
- È più probabile che
esca un `sei'' su 4 lanci di un dado
o un ``doppio sei'' su 24 lanci di due dadi?
(Questo è uno dei problemi classici della probabilità
proposto dal Cavalier de Méré a Pascal.)
- Quante volte bisogna lanciare un dado per essere sicuri al
99% che esca una certa faccia?
- In relazione al problema precedente: quanto vale la probabilità
che la faccia prescelta si verifichi al venticinquesimo lancio
se non si è verificato nei precedenti ventiquattro?
Dare sia la risposta intuitiva
che quella che si ottiene valutando
- Ai tre eventi
mutualmente incompatibili
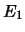 ,
, 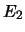 ed
ed 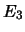 vengono assegnate probabilità
vengono assegnate probabilità 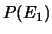 ,
, 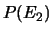 e
e 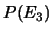 (ad esempio, rispettivamente 10, 20 e 30%).
Mostrare come la probabilità
di ciascuno degli eventi, subordinata al
verificarsi di uno dei tre, è
pari a
(ad esempio, rispettivamente 10, 20 e 30%).
Mostrare come la probabilità
di ciascuno degli eventi, subordinata al
verificarsi di uno dei tre, è
pari a
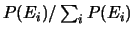 .
.
- Tre amici (
 ntonio,
ntonio,  erto e
erto e 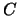 arlo)
scommettono sull'uscita del numero 51 sulla ruota di Venezia.
I termini della scommessa sono i seguenti: se il numero esce
alla prima settimana di attesa vince
arlo)
scommettono sull'uscita del numero 51 sulla ruota di Venezia.
I termini della scommessa sono i seguenti: se il numero esce
alla prima settimana di attesa vince  , se esce alla seconda settimana
vince
, se esce alla seconda settimana
vince  , se alla terza vince
, se alla terza vince 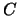 . Se il numero non esce entro le prime
tre settimane la scommessa viene invalidata. Chi ha maggiore probabilità
di vincere la scommessa?
Quanto
devono puntare
. Se il numero non esce entro le prime
tre settimane la scommessa viene invalidata. Chi ha maggiore probabilità
di vincere la scommessa?
Quanto
devono puntare  e
e 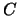 se
se  punta
punta
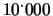 lire,
affinché la scommessa sia equa?
lire,
affinché la scommessa sia equa?
- Un quotidiano4.6
pubblica i pronostici per il totocalcio riportati nella seguente tabella,
espressi in probabilità (in %) dei diversi segni (per curiosità
è riportata anche la schedina vincente).
Il giornalista si era basato,
apparentemente, su sole considerazioni
tecniche4.7.
| |
1 |
X |
2 |
Ris. |
| 1 |
20 |
40 |
40 |
1 |
| 2 |
30 |
25 |
45 |
1 |
| 3 |
40 |
25 |
35 |
X |
| 4 |
45 |
20 |
35 |
1 |
| 5 |
50 |
20 |
30 |
1 |
| 6 |
45 |
35 |
20 |
X |
| 7 |
40 |
35 |
25 |
2 |
| 8 |
60 |
30 |
10 |
1 |
| 9 |
35 |
40 |
25 |
1 |
| 10 |
30 |
25 |
45 |
X |
| 11 |
35 |
40 |
25 |
2 |
| 12 |
35 |
30 |
35 |
2 |
| 13 |
45 |
35 |
20 |
X |
Valutare la probabilità della(e) colonna(e) ritenuta(e)
più probabile(i) e meno probabile(i). Confrontare con quanto si
otterrebbe se tutti i segni avessero la stessa probabilità.
È più probabile la colonna con tutti 1 o la colonna ``12X12X12X12X1''?
- Ammettiamo che due amici (
 e
e  ) concordino con i pronostici
del problema precedente e vogliano fare la seguente scommessa:
) concordino con i pronostici
del problema precedente e vogliano fare la seguente scommessa:
 punta su tutti segni 1 e
punta su tutti segni 1 e  punta una sequenza alternata di 1 e X, a partire da 1.
Se non si verifica nessuno dei due eventi la scommessa è invalidata.
Quanto deve puntare ciascuno affinché la scommessa sia equa?
punta una sequenza alternata di 1 e X, a partire da 1.
Se non si verifica nessuno dei due eventi la scommessa è invalidata.
Quanto deve puntare ciascuno affinché la scommessa sia equa?
- In un cassetto sono riposti
disordinatamente 10 calzini bianchi, 10 rossi e 10 neri.
Quanto vale la probabilità che,
alzandosi la mattina al buio e prendendo due calzini a caso,
se ne estraggano due dello stesso colore? E se se ne prendono
3? Quanti calzini bisogna prendere per avere la certezza
che fra di essi ve ne siano due dello stesso colore?
Quanto vale invece la probabilità che estraendo 4 calzini ce ne
siano almeno due del colore del primo calzino estratto?
Dopo quanti calzini si ha la certezza di avere almeno due
calzini dello stesso colore del primo estratto?
- Qual'è la probabilità che giocando a tressette (gioco italiano da
40 carte) un giocatore non
riceva nemmeno un ``pezzo''? (A questo gioco si chiamano
pezzi l'Asso, il Due e il Tre). Qual'è la probabilità che
questo capiti ad almeno due giocatori? E a tre?
- Riprendiamo il problema 4 del capitolo 1
delle due scatole di cui una contiene
8 palline bianche e 2 nere e l'altra
2 bianche e 8 nere.
Si estrae una pallina da una scatola
scelta a caso e,
senza guardarla, la si ripone nell'altra scatola.
Successivamente si estrae
una pallina da quest'ultima scatola. Calcolare la probabilità
che la pallina sia bianca facendo i conti dettagliati.
- In una razza di cani il gene
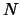 che determina il mantello nero domina su quello responsabile
del mantello
rosso (gene
che determina il mantello nero domina su quello responsabile
del mantello
rosso (gene  ). Una cagna nera dal genotipo eterozigote (
). Una cagna nera dal genotipo eterozigote (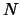 ,
,  )
viene incrociata con un maschio nero avente lo stesso genotipo.
Quanto vale la probabilità che su 5 cuccioli non ce ne
sia nemmeno uno rosso? (Trascurare la possibilità di
gemelli monoovulari.)
)
viene incrociata con un maschio nero avente lo stesso genotipo.
Quanto vale la probabilità che su 5 cuccioli non ce ne
sia nemmeno uno rosso? (Trascurare la possibilità di
gemelli monoovulari.)
- Una persona fa il seguente ragionamento per calcolare la
probabilità che ci sia vita animale su Marte
(la storiella è antecedente
le missiomi spaziali): siccome non so niente, la probabilità
che ci siano i felini è del 50%; ugualmente c'è il 50%
di probabilità che ci siano rettili; e così via. Ne segue che
considerando
 specie animali, la probabilità che non ce ne sia
nessuna è pari a
specie animali, la probabilità che non ce ne sia
nessuna è pari a 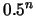 , da cui segue che
, da cui segue che
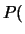 vita
vita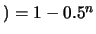 . Quindi
la probabilità di vita tende a 1 pur di considerare un numero
se il ragionamento viene esteso
a molte specie specie. Questa amenità viene presentata da taluni
come un paradosso derivante dall'uso della probabilità soggettiva.
Dove stanno gli errori di ragionamento?
. Quindi
la probabilità di vita tende a 1 pur di considerare un numero
se il ragionamento viene esteso
a molte specie specie. Questa amenità viene presentata da taluni
come un paradosso derivante dall'uso della probabilità soggettiva.
Dove stanno gli errori di ragionamento?
- Una persona ritiene che la probabilità che una squadra vinca un'incontro
di calcio sia dell'80%, mentre la probabilità che
essa termini
il primo tempo in vantaggio
sia del 60%. Inoltre valuta nel 90% la probabilità che
la squadra
vinca l'incontro qualora cominci in vantaggio il secondo tempo.
Quanto vale la probabilità che essa vinca l'incontro pur non essendo
in vantaggio al primo tempo?
- Riferendosi al labirinto
di figura 4.4: quanto vale la probabilità
di arrivare al tesoro e uscire vivi?
- Consideriamo il problema 33 del capitolo 2. Quanto vale la probabilità
che entrambe le palline siano dello stesso colore se riteniamo
che la procedura di preparazione sia al 70% la prima descritta
nella soluzione di tale problema e al 30% la seconda?
- Riprendiamo il problema 25 del capitolo
2: si immagini che
che il concorrente non si fidi del presentatore e pensi che
possa aver bluffato. È ancora conveniente cambiare scatola?
Ad esempio quanto vale la probabilità
che il premio sia nell'altra scatola
se crede al 50% che il presentatore possa aver bluffato?
- Quanto vale la probabilità che il secondo estratto
al lotto sia il 25? (Si consiglia di usare, anche se non è strettamente
necessario, la legge delle alternative).
- Quanto vale la probabilità che il terzo estratto sia il 16,
nell'ipotesi che il secondo estratto sia il 47?
E se si venisse a sapere anche che il primo estratto era il 58?
- Ancora sui problemi 24 e 25 del capitolo 2:
Risolvere i problemi in modo più formale usando
la legge delle alternative.




Next: Probabilità delle cause e
Up: Regole della probabilità
Previous: Ricapitolando
Indice
Giulio D'Agostini
2001-04-02
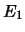 = ``si verifica soltanto
= ``si verifica soltanto  '';
'';
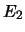 = ``si verificano sia
= ``si verificano sia  che
che  che
che 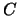 '';
'';
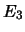 = ``non si verifica né
= ``non si verifica né  , né
, né  , né
, né 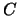 '';
'';
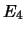 = ``si verifica almeno uno degli eventi'';
= ``si verifica almeno uno degli eventi'';
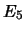 = ``si verificano al più due eventi'';
= ``si verificano al più due eventi'';
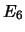 = ``si verificano
= ``si verificano  e
e  , indipendentemente dall'esito di
, indipendentemente dall'esito di 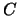 '';
'';
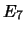 = ``si verifica
= ``si verifica  indipendentemente dall'esito degli altri'';
indipendentemente dall'esito degli altri'';
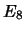 = ``si verifica
= ``si verifica  , ma non
, ma non  , indipendentemente dall'esito
di
, indipendentemente dall'esito
di 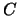 '';
'';
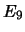 = ``si verificano tutti o (``OR'') nessuno degli eventi''
= ``si verificano tutti o (``OR'') nessuno degli eventi''
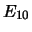 = ``si verifica
= ``si verifica  indipendentemente dagli altri due,
o (``OR'') si verifica
uno degli altri due''
indipendentemente dagli altri due,
o (``OR'') si verifica
uno degli altri due''
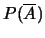 ;
;
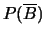 ;
;
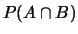 ;
;
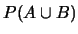 ;
;
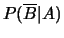 ;
;
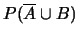 ;
;
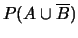 ;
;
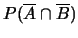 ;
;
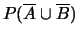 ;
;
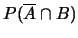 ;
;
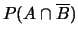 ;
;
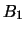 ;
;
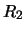 ;
;
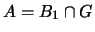 ;
;
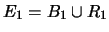 ;
;
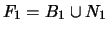
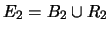 ;
;
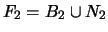 ;
;
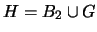 .
.
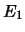 e
e 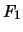 ;
;
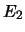 e
e 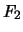 ;
;
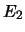 e
e 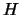 ;
;
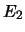 ,
, 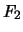 e
e 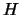 .
.