


Next: The extraction of the
Up: A measurement of the
Previous: Introduction
The measurement of the 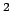 structure function is equivalent to
the measurement of the differential cross section
structure function is equivalent to
the measurement of the differential cross section
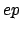 .
Therefore,
we need to unfold
the measured distribution to get the (``true'') number of the
events in the selected bins.
Known the
.
Therefore,
we need to unfold
the measured distribution to get the (``true'') number of the
events in the selected bins.
Known the 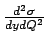 , the likelihood
that effect
, the likelihood
that effect 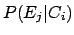 (an observed event reconstructed in the bin
(an observed event reconstructed in the bin 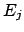 )
is due to cause
)
is due to cause 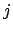 , and
, and 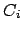 ,
the measured number of events in the bin
,
the measured number of events in the bin 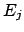 ,
the unfolded number of events due to the
,
the unfolded number of events due to the 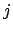 is
given by:
is
given by:
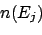 |
(1) |
where
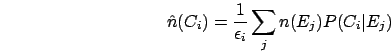 is the
efficiency of detecting an event generated by
is the
efficiency of detecting an event generated by 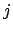 .
The elements
.
The elements 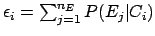 are calculated by the Bayes' theorem:
are calculated by the Bayes' theorem:
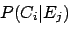 |
(2) |
Giulio D'Agostini
2004-05-05
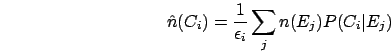 is the
efficiency of detecting an event generated by
is the
efficiency of detecting an event generated by