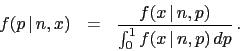- ... communication1
- Note based on lectures
at the University of Perugia, 15-16 April 2011
and at MAPSES School in Lecce, 23-25 November 2011
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Columbo',2
- Besides
the inappropriate
reference to the Columbo's episode,
I consider that article
substantially well done and I recommend its reading.
To those interested in the subject ``probability and the law''
I also recommend, as starting points for further navigation,
refs. [4].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
`data',3
- For non experts it is important to clarify,
although this is not deeply relevant here, that the histogram's
`data' are non simple `empirical observations', but
a result of selections and analysis (including calibrations),
after suitable definitions of
physical objects, like what a `jet' is.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... events4
- This number,
as well as 230 that follows,
was estimated from the figure
- precise numbers are
irrelevant for the purpose of this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `arithmetically'.5
- It seems rather
natural to think that, if the
purpose of a `subtraction' would be that of
highlight extra physical components in the spectrum,
this procedure should not be simply
an `arithmetic subtraction'
and, in particular, it should not yield
unphysical negative counts.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... statistic.6
- Let us remind
that if a variable is described by a
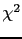 distribution
with
distribution
with 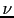 degrees of freedom, our (probabilistic)
expectation (`expected value') is
degrees of freedom, our (probabilistic)
expectation (`expected value') is 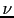 , with
expectation uncertainty (`standard deviation')
, with
expectation uncertainty (`standard deviation') 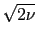 .
Hence if
.
Hence if 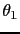 and
and 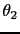 are variables of that
kind, with
are variables of that
kind, with 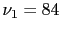 and
and 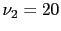 , our
expectations will be ``
, our
expectations will be ``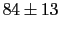 '' and
``
'' and
``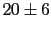 '', respectively.
(As a side remark, we notice
that, that adding a Gaussian component to explain
the `excess', the difference between expected and observed
value of the test statistic increases,
since the
'', respectively.
(As a side remark, we notice
that, that adding a Gaussian component to explain
the `excess', the difference between expected and observed
value of the test statistic increases,
since the 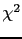 goes to 56.7 for the entire region and 10.9 for
the `peak region'.)
goes to 56.7 for the entire region and 10.9 for
the `peak region'.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... right.7
- After years
of practice in particle physics and related subjects,
I have developed my rule of the thumb, which until now
has never failed: ``the funnier is the name of the test
used to show that there is a disagreement with the
`Standard Model' (or whatever is considered
firmly established), the
less I believe that this is the case''
(with the corollary that ``in the future I will tend to
mistrust those people'').
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... courses.8
- Having written quite a lot on the subject,
I don't want to go through yet another introduction
to the subject and refer to the
`Columbo paper'[5] (someone might find useful
also [14]), only reminding here some of the
basic ideas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... GeV,''9
- By the way it was about 36% percent by the
best or our knowledge at the beginning of
1999[18],
and it has changed with time,
especially during 2011!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... something.10
- For example, when
I ask about the meaning of 95% CL lower bound on Higgs mass
from LEP direct search, practically everybody - and I speak
of particle physicists! - `explains' the result in
probabilistic terms[20],
although it is well known to
frequentistic experts that
``The lower bounds on the Higgs mass that are quoted for
the direct Higgs searches at LEP say absolutely
nothing about the probability of the Higgs mass being
higher or lower than some value.''[21]
(By the way, it seems that the method
described in [21] is essentially the one on which
the LHC collaborations have agreed to report search limits:
at least you know now what these results (do not) mean!)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... false.11
- If you want to try,
you can play with The ultimate confidence intervals
calculator[23]
and no strict follower of Neyman's teaching can
blame you of the results, that asymptotically will `cover'
the true value of whatever quantity
you have in mind in exactly the proportion of times
you pre-define.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... mistakes.12
- For example,
in 2000 there was some excitement at CERN because some LEP experiments
were observing some events above the expectation and there was
a big action against the CERN directorate, that had decided
to stop LEP in order to use structures and human/financial resources
for LHC.
This was an email I received
the 10th of November 2000,
addressed to a short list of physicists:
Subject: Do you want the Higgs found next year?
As you may know CERN DG, L.Maiani, has decided to shut
off LEP. The decision is to be confirmed at a CERN Committee of
Council meeting on Friday 17th.
As you probably know there is evidence for a Standard Model Higgs
boson seen in the data in the last few months, with a probability
as a background fluctuation of 4 per mille, or 2.9 sigma.
...
In other words we are seeing exactly what we should expect if Mh=115.
...
[If you wonder why 2.9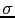 's is 4 per mille, instead of 2,
don't ask me.]
's is 4 per mille, instead of 2,
don't ask me.]
The message ended with a request to write to Maiani in support
of extending LEP run. Here follows my instant reply:Let me understand:
do you REALLY feel 99.6% sure that the Higgs is around 115GeV
(let's say below the effective kinematical threshold at the present
LEP energy)? If not, how much are you confident?
...
Running or not running is a delicate decision problem which involves
beliefs and risks (both financial and sociological). Therefore,
I cannot disagree much with Maiani, being in his position.
On the other hand, in the position of any LEP collaborator I would
push to run, certainly! (Given the same beliefs, the risk
analysis is completely different).
Being myself neither the CERN Director-General, or a LEP
physicist, but, with this respect, just a physics educated tax payer,
I find myself more on the side of Maiani than on that of our
LEP colleagues.
To make it clear, the ``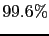 '' could not be how much
we had to rationally believe the Higgs was at 115GeV, because
it was a 0.004 p-value incorrectly turned into probability.
Estimating correctly the probability, one would have got
a few percent (see e.g. [18] for the
method, although the numbers had changed in the meanwhile).
And with a few percent, it would have been crazy to continue the LEP
run, delay LHC and so on. On the other hand, if there was really
a 99.6% probability, then LEP had to go on. (As it often happens
with misinterpreted frequentistic methods, the errors are not
little, like getting 99.6 for what should have better been 99.1,
98.5, or even perhaps 97%! - see chapter 1 of [6] for other examples.
Here one considered practically certain something that was instead
almost impossible.)
'' could not be how much
we had to rationally believe the Higgs was at 115GeV, because
it was a 0.004 p-value incorrectly turned into probability.
Estimating correctly the probability, one would have got
a few percent (see e.g. [18] for the
method, although the numbers had changed in the meanwhile).
And with a few percent, it would have been crazy to continue the LEP
run, delay LHC and so on. On the other hand, if there was really
a 99.6% probability, then LEP had to go on. (As it often happens
with misinterpreted frequentistic methods, the errors are not
little, like getting 99.6 for what should have better been 99.1,
98.5, or even perhaps 97%! - see chapter 1 of [6] for other examples.
Here one considered practically certain something that was instead
almost impossible.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... probability.13
- But if you really
have the chance of making real bets, don't use the fair
odds: you want to maximize the expected gain! This is what
insurance companies and professional bookmakers do:
evaluate the fair odds and then propose the most unfair ones
in a given direction,
unbalanced as much as someone can still accept them.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... principle'14
- In the Essai
`principles' do no stand for what we mean now
as `first principles', or `axioms',
but are rather the fundamental rules of probability
that Laplace had derived elsewhere.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... likelihood15
- Note that
here likelihood is the same as probability, and has nothing
to do with what statisticians call `likelihood' - reading
directly the original French version might help,
also taking into account
that two hundred years ago the nouns were not as specialized
as they now are.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
trials16
- In modern terms,
the problem solved by Bayes in a quite convoluted notation
[29] was the inference of the
binomial parameter
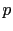 , conditioned on
, conditioned on 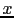 successes in
successes in 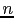 trials, under the assumption that all values of
trials, under the assumption that all values of 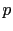 were a priori equally likely
were a priori equally likely
Laplace solved independently this problem and, indeed, the
formula that gives the expected value of 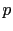 , i.e.
, i.e.
is known as Laplace's rule
of succession.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 114 GeV;17
- As mentioned in
footnote 9, the 95% CL bound
has nothing to do with 95% probability that its value
was above the bounds. Translating the experimental
information from the direct search into probabilistic
assessments is not that easy, because the number
also depends on the upper limits. In particular,
if there would be `no' upper bound on the mass
(that obviously cannot weigh grams!) there is no way
to calculate the required probability. For further
details see [18] and chapter 13 of
[6].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
elsewhere.18
- And if it wouldn't exist at all?
OK, formulate the alternative model and
try to assess your beliefs in the
alternatives.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Times:19
- I definitely
hope that when this influential newspaper reports on probability of
important, uncertain scenarios that really matter for our lives,
such as economy, health,
international crises, future of the Planet and so
on, its experts really know what they are talking about!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.