



Next: Probability of the causes
Up: Uncertainty in physics and
Previous: Usual handling of measurement
Contents
The criticism about
the inconsistent interpretation
of results
may look like a philosophical quibble,
but it is, in my opinion, a crucial point
which needs to be clarified.
Let us consider the
example
of  independent measurements
of the same quantity under identical conditions (with
independent measurements
of the same quantity under identical conditions (with  large
enough to simplify the problem,
and neglecting systematic effects).
We can evaluate the arithmetic average
large
enough to simplify the problem,
and neglecting systematic effects).
We can evaluate the arithmetic average
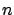 and the
standard deviation
and the
standard deviation 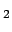 . The result on the true value
. The result on the true value  is
is
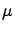 |
(1.2) |
The reader will have no difficulty in admitting
that the large
majority of people interpret (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
as if it were1.7
)
as if it were1.7
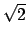 |
(1.3) |
However, conventional statistics says only
that1.8
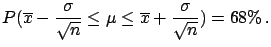 |
(1.4) |
a probabilistic statement about
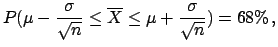 , given
, given  ,
,
 and
and  . Probabilistic statements
concerning
. Probabilistic statements
concerning  are not foreseen by the theory (``
are not foreseen by the theory (`` is a constant of unknown
value''1.9), although
this is what we are, intuitively, looking for:
Having observed the effect
is a constant of unknown
value''1.9), although
this is what we are, intuitively, looking for:
Having observed the effect
 we are interested
in stating something about the possible
true value responsible for it.
In fact, when
we do an experiment, we want to increase
our knowledge about
we are interested
in stating something about the possible
true value responsible for it.
In fact, when
we do an experiment, we want to increase
our knowledge about  and, consciously or not,
we want to know which values are more or less probable.
A statement concerning the probability
that an observed value falls within a certain interval around
and, consciously or not,
we want to know which values are more or less probable.
A statement concerning the probability
that an observed value falls within a certain interval around  is meaningless if it cannot be turned into an expression which states the
quality of the knowledge about
is meaningless if it cannot be turned into an expression which states the
quality of the knowledge about  itself.
Since the usual probability theory does not help, the probability
inversion is performed intuitively. In routine cases it usually
works,
but there are cases in which it fails (see Section
itself.
Since the usual probability theory does not help, the probability
inversion is performed intuitively. In routine cases it usually
works,
but there are cases in which it fails (see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).




Next: Probability of the causes
Up: Uncertainty in physics and
Previous: Usual handling of measurement
Contents
Giulio D'Agostini
2003-05-15