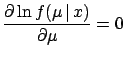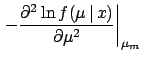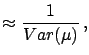Next: Evaluation of uncertainty: general
Up: A probabilistic theory of
Previous: Afraid of `prejudices'? Inevitability
Contents
Recovering standard methods
and short-cuts to Bayesian reasoning
Before moving on to applications, it is necessary to
answer an important question: ``Should one proceed by
applying Bayes' theorem in every situation?''
The answer is no, and the alternative is essentially
implicit in (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ), and can be paraphrased
with the example of
the dog and the hunter.
), and can be paraphrased
with the example of
the dog and the hunter.
We have already used this example
in Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ,
when we were discussing
the arbitrariness of probability inversion performed
unconsciously by (most of)2.13
those who use the scheme of
confidence intervals. The same example will also be used in
Section
,
when we were discussing
the arbitrariness of probability inversion performed
unconsciously by (most of)2.13
those who use the scheme of
confidence intervals. The same example will also be used in
Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , when discussing the reason why Bayesian estimators
appear to be distorted (a topic discussed in more detail in
Section
, when discussing the reason why Bayesian estimators
appear to be distorted (a topic discussed in more detail in
Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
This analogy is very important,
and, in many practical applications, it allows us
to bypass the explicit
use of Bayes' theorem when priors
do not sizably influence the result
(in the case of a normal model the demonstration can be seen
in Section
).
This analogy is very important,
and, in many practical applications, it allows us
to bypass the explicit
use of Bayes' theorem when priors
do not sizably influence the result
(in the case of a normal model the demonstration can be seen
in Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
).
Figure:
Relation between Bayesian inference and standard
data analysis methods. The top-down flow shows subsequent
limiting conditions. For an understanding of the relation
between the `normal' 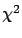 and the Pearson
and the Pearson 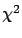 Ref. [24]
is recommended.
Ref. [24]
is recommended.
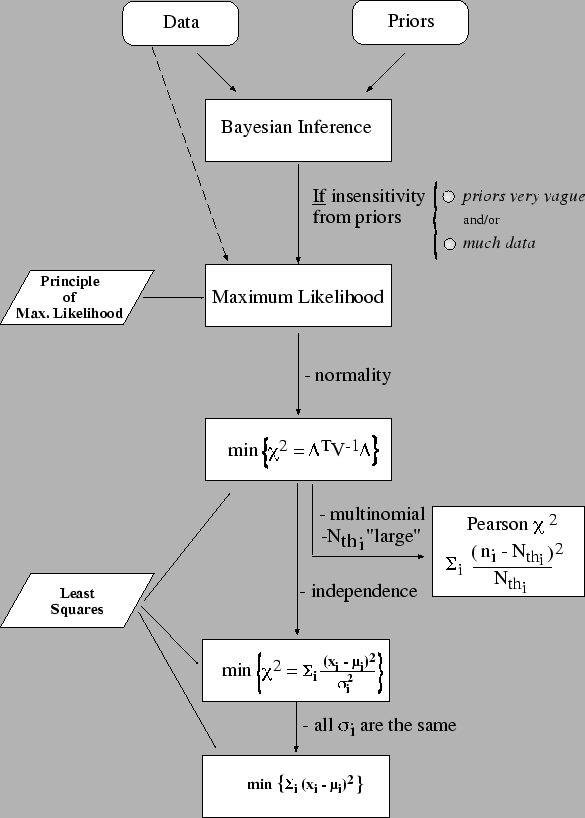 |
Figure ![[*]](file:/usr/lib/latex2html/icons/crossref.png) shows how it is possible to recover
standard methods from a Bayesian perspective.
One sees that the crucial link is with the Maximum Likelihood Principle,
which, in this approach is just a subcase (see Section
shows how it is possible to recover
standard methods from a Bayesian perspective.
One sees that the crucial link is with the Maximum Likelihood Principle,
which, in this approach is just a subcase (see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
Then, when extra simplifying restrictions
are verified, the different forms
of the Least Squares are reobtained. In conclusion:
).
Then, when extra simplifying restrictions
are verified, the different forms
of the Least Squares are reobtained. In conclusion:
- One is allowed to
use these methods if one thinks that the approximations
are valid; the same happens with the usual propagation of
uncertainties and of their correlations,
outlined in the next section.
- One keeps the Bayesian interpretation of the results; in particular,
one is allowed to talk about the probability distributions of the
true values, with all the philosophical and practical advantages
we have seen.
- Even if the priors are
not negligible, but the final distribution
is roughly normal,2.14 one can evaluate the
expected value and standard deviation
from the shape of the distribution,
as is well known:
where 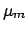 stands for the mode of the distribution.
stands for the mode of the distribution.




Next: Evaluation of uncertainty: general
Up: A probabilistic theory of
Previous: Afraid of `prejudices'? Inevitability
Contents
Giulio D'Agostini
2003-05-15
![]() ,
when we were discussing
the arbitrariness of probability inversion performed
unconsciously by (most of)2.13
those who use the scheme of
confidence intervals. The same example will also be used in
Section
,
when we were discussing
the arbitrariness of probability inversion performed
unconsciously by (most of)2.13
those who use the scheme of
confidence intervals. The same example will also be used in
Section ![]() , when discussing the reason why Bayesian estimators
appear to be distorted (a topic discussed in more detail in
Section
, when discussing the reason why Bayesian estimators
appear to be distorted (a topic discussed in more detail in
Section ![]() ).
This analogy is very important,
and, in many practical applications, it allows us
to bypass the explicit
use of Bayes' theorem when priors
do not sizably influence the result
(in the case of a normal model the demonstration can be seen
in Section
).
This analogy is very important,
and, in many practical applications, it allows us
to bypass the explicit
use of Bayes' theorem when priors
do not sizably influence the result
(in the case of a normal model the demonstration can be seen
in Section ![]() ).
).