



Next: Central limit theorem
Up: Random variables
Previous: Continuous variables: probability and
Contents
We only consider the case of two continuous variables ( and
and 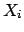 ).
The extension to more variables is straightforward.
The infinitesimal element of probability is
).
The extension to more variables is straightforward.
The infinitesimal element of probability is
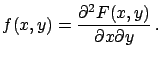 , and the probability
density function
, and the probability
density function
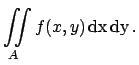 |
(4.43) |
The probability of finding the variable inside a certain
area  is
is
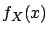 |
(4.44) |
- Marginal distributions:
-
The subscripts  and
and 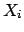 indicate that
indicate that
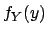 and
and 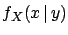 are only functions of
are only functions of
 and
and 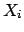 , respectively (to avoid fooling around with different
symbols to indicate the generic function), but in most cases
we will drop the subscripts if the context helps in resolving
ambiguities.
, respectively (to avoid fooling around with different
symbols to indicate the generic function), but in most cases
we will drop the subscripts if the context helps in resolving
ambiguities.
- Conditional distributions:
-
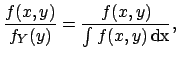 |
 |
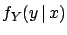 |
(4.47) |
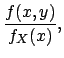 |
 |
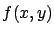 |
(4.48) |
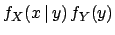 |
 |
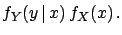 |
(4.49) |
| |
 |
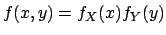 |
(4.50) |
- Independent random variables
-
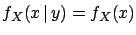 |
(4.51) |
(it implies
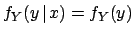 and
and
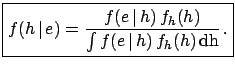 .)
.)
- Bayes' theorem for continuous random variables
-
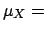 |
(4.52) |
(Note added: see proof in section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .)
.)
- Expectation value:
-
and analogously for 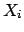 . In general
. In general
E![$\displaystyle [g(X,Y)] = \int\!\!\int_{-\infty}^{+\infty} \!g(x,y)\, f(x,y)\, \rm {d}x\,\rm {d}y\,.$](img507.png) |
(4.55) |
- Variance:
-
and analogously for 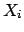 .
.
- Covariance:
-
If  and
and 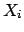 are independent, then
E
are independent, then
E![$ [XY]=$](img516.png) E
E![$ [X]\cdot$](img517.png) E
E![$ [Y]$](img518.png) and hence
Cov
and hence
Cov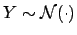 (the opposite is true only if
(the opposite is true only if  ,
,
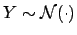 ).
).
- Correlation coefficient:
-
- Linear combinations of random variables:
-
If
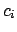 , with
, with 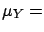 real, then:
real, then:
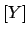 E E![$\displaystyle [Y]$](img528.png) |
 |
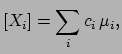 E E![$\displaystyle [X_i] = \sum_ic_i\,\mu_i,$](img530.png) |
(4.61) |
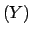 Var Var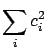 |
 |
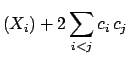 Var Var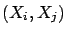 Cov Cov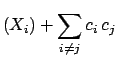 |
(4.62) |
| |
 |
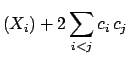 Var Var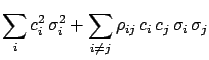 Cov Cov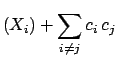 |
(4.63) |
| |
 |
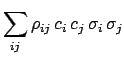 |
(4.64) |
| |
 |
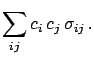 |
(4.65) |
| |
 |
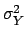 |
(4.66) |
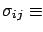 has been written in different ways, with
increasing levels of compactness, that can be found
in the literature. In particular, (
has been written in different ways, with
increasing levels of compactness, that can be found
in the literature. In particular, (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and
(
) and
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) use the notations
) use the notations
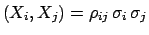 Cov
Cov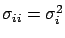 and
and
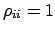 , and the fact that,
by definition,
, and the fact that,
by definition,
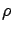 .
.
- Bivariate normal distribution:
-
Joint probability density function
of  and
and 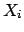 with correlation coefficient
with correlation coefficient 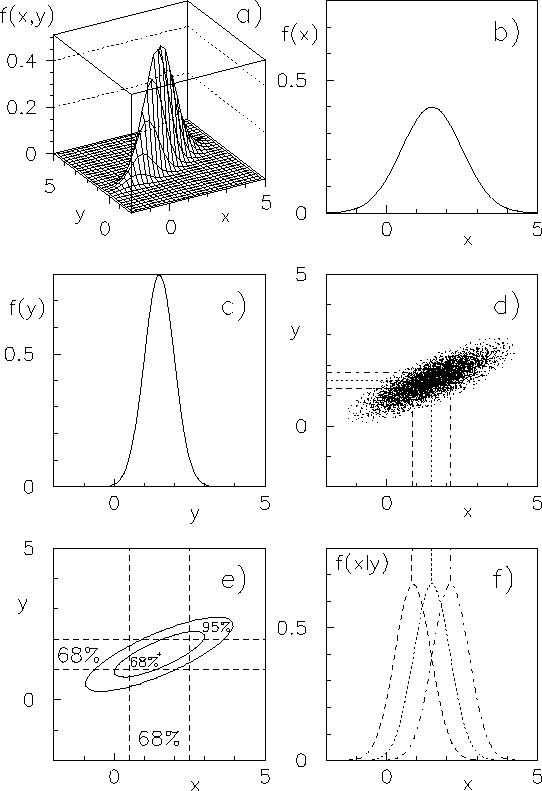 (see Fig.
(see Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ):
):
Figure:
Example of bivariate normal distribution.
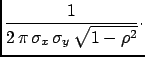 |
Marginal distributions:
Conditional distribution:
![$\displaystyle f(y\,\vert\,x_\circ) = \frac{1}{\sqrt{2\,\pi}\,\sigma_y\,\sqrt{1-...
...(x_\circ-\mu_x\right)\right] \right)^2} {2\,\sigma_y^2\,(1-\rho^2)} \right]}\,,$](img554.png) |
(4.70) |
i.e.
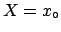 |
(4.71) |
The condition 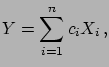 squeezes the standard deviation and shifts
the mean of
squeezes the standard deviation and shifts
the mean of 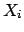 .
.




Next: Central limit theorem
Up: Random variables
Previous: Continuous variables: probability and
Contents
Giulio D'Agostini
2003-05-15
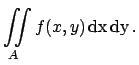
 and
and 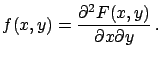 , and the probability
density function
, and the probability
density function
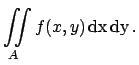
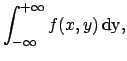
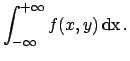
 and
and  and
and 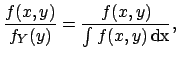
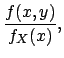
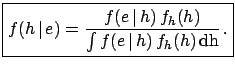 .)
.)
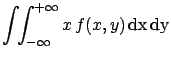 E
E![$\displaystyle [X]$](img452.png)
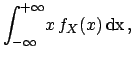
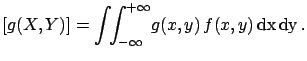
 and
and  ,
,
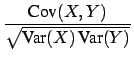
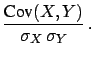
 and
and  (see Fig.
(see Fig. 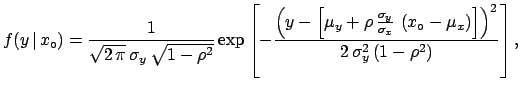
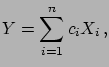 squeezes the standard deviation and shifts
the mean of
squeezes the standard deviation and shifts
the mean of