



Next: Normal distribution of measurement
Up: Central limit theorem
Previous: Distribution of a sample
Contents
Another important application of the theorem is that the binomial
and the Poisson distribution can be approximated, for ``large numbers'',
by a normal distribution. This is a general result, valid for
all distributions which have the reproductive property
under the sum. Distributions of this kind are the binomial,
the Poisson and the 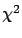 . Let us go into more detail:
. Let us go into more detail:
-
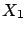
- The reproductive property of the binomial states that if
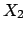 ,
,
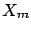 ,
,  ,
, 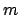 are
are 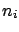 independent variables,
each following a binomial distribution of parameter
independent variables,
each following a binomial distribution of parameter 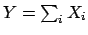 and
and 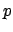 ,
then their sum
,
then their sum
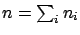 also follows a binomial distribution
with parameters
also follows a binomial distribution
with parameters
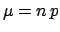 and
and 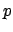 . It is easy to be convinced
of this property without
any mathematics. Just think of what happens if one tosses bunches
of three, of five and of ten coins, and then one considers
the global result:
a binomial with a large
. It is easy to be convinced
of this property without
any mathematics. Just think of what happens if one tosses bunches
of three, of five and of ten coins, and then one considers
the global result:
a binomial with a large  can then always
be seen as a sum of many binomials with smaller
can then always
be seen as a sum of many binomials with smaller 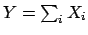 . The
application of the central limit theorem is straightforward,
apart from deciding when the convergence is acceptable.
The parameters on which one has to base a judgment
are in this case
. The
application of the central limit theorem is straightforward,
apart from deciding when the convergence is acceptable.
The parameters on which one has to base a judgment
are in this case 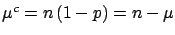 and the
complementary quantity
and the
complementary quantity
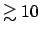 . If they are
both
. If they are
both
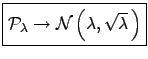 then the approximation starts to
be reasonable.
then the approximation starts to
be reasonable.
-
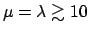
- The same argument holds for the Poisson distribution.
In this case the approximation starts to be reasonable
when
 .
.




Next: Normal distribution of measurement
Up: Central limit theorem
Previous: Distribution of a sample
Contents
Giulio D'Agostini
2003-05-15
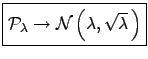 then the approximation starts to
be reasonable.
then the approximation starts to
be reasonable.
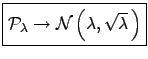 then the approximation starts to
be reasonable.
then the approximation starts to
be reasonable.