



Next: Use and misuse of
Up: Building the covariance matrix
Previous: Normalization uncertainty
Contents
Let us assume there are  independently
measured values
independently
measured values 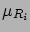 and
and
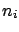 calibration constants
calibration constants 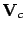 with their covariance matrix
with their covariance matrix
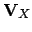 . The latter
can also be theoretical parameters influencing the data, and
moreover they may be
correlated, as usually
happens if, for example, they are parameters of a calibration fit.
We can then include the
. The latter
can also be theoretical parameters influencing the data, and
moreover they may be
correlated, as usually
happens if, for example, they are parameters of a calibration fit.
We can then include the 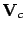 in the vector that contains the
measurements and
in the vector that contains the
measurements and 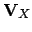 in the covariance matrix
in the covariance matrix 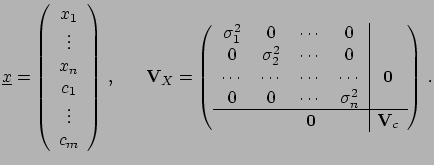 :
:
 |
(6.44) |
The corrected quantities are obtained from the most general
function
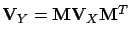 |
(6.45) |
and the covariance matrix
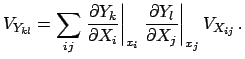 from the covariance propagation
from the covariance propagation
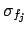 .
.
As a frequently encountered example, we can think of several
normalization constants, each affecting a subsample of the data -
as is
the case where each of several detectors
measures a set of physical quantities.
Let us consider just three quantities
( ) and three
uncorrelated
normalization standard uncertainties (
) and three
uncorrelated
normalization standard uncertainties (
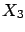 ),
the first common to
),
the first common to
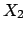 and
and 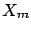 , the second to
, the second to
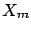 and
and 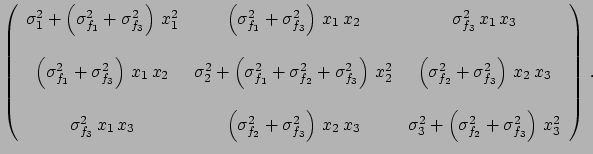 and the third to all three.
We get the following covariance matrix:
and the third to all three.
We get the following covariance matrix:
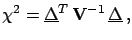 |
(6.46) |




Next: Use and misuse of
Up: Building the covariance matrix
Previous: Normalization uncertainty
Contents
Giulio D'Agostini
2003-05-15
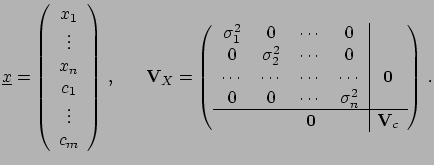 :
:
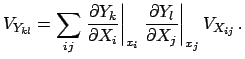 from the covariance propagation
from the covariance propagation
 ) and three
uncorrelated
normalization standard uncertainties (
) and three
uncorrelated
normalization standard uncertainties (
![]() ),
the first common to
),
the first common to
![]() and
and ![]() , the second to
, the second to
![]() and
and 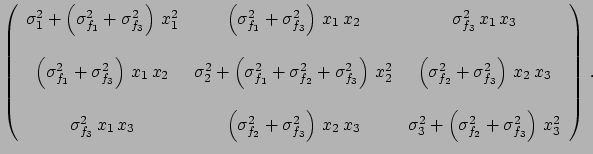 and the third to all three.
We get the following covariance matrix:
and the third to all three.
We get the following covariance matrix: