- ...m/s.1
- A meter
is the distance covered
by light in vacuum in
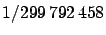 of a second.
of a second.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... wave.2
- A second is
equal to the duration of
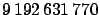 periods of the
radiation corresponding to the transition between two hyperfine levels
(F=4, M=0 and F=3, M=0 of the fundamental status
periods of the
radiation corresponding to the transition between two hyperfine levels
(F=4, M=0 and F=3, M=0 of the fundamental status  )
of the atom Cesium 133.
)
of the atom Cesium 133.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
quantity'' 3
- All English quotes not
referring to English bibliography are translation
by the authors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... '' 4
- The earliest
measurement standard we have evidence of
is the Egyptian cubit,
the length of the forearm from elbow to fingers,
realized around 2500 B.C. in a piece of marble of about 50
centimeters [5].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... system,5
- With
this respect, changes of currencies
are easily ruled by central banks,
especially in modern times in which banknotes and coins have no
intrinsic value.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fiasco.6
- In history
there are plenty of examples of
this kind, like the difficulty of France to establish
the decimal metric system
or the failed Carolingian and Renaissance reforms [9].
Just to make a recent and practical example,
Italy has adopted the International System (SI) since
the mid seventies,
and other units were banned by law. Nevertheless,
after thirty years, though the SI unit of power is the Watt,
car power is quoted in HP (yes, official
documents do have kW, but drivers, sellers and media only
speak of HP), centralized home heating power in kCal/h,
(but small electric heaters are given in Watt)
and air conditioning cooling power in Btu/h.
What is bad is that, contrary to
centimeters and inches, where people know that the units
measure the same thing but citizens of
different countries have a mental representation in
either unit, the average Italian does not even know that all
the above units measure the same thing
and practically none has
a mental representation of a Btu/h, arrived to us
in mass with air conditioners in the last few years.
Therefore, people don't even suspect that it is possible
to convert Btu/h to Watt
to have a better perception of what 7000 Btu/h might mean
(a cooling power of about 2kW).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
others.7
- For example, this was one of the possibilities
envisaged in France before the metric system: to extend to all France
the system used in Paris. This was still the proposal of
Joseph-Jérôme Lalande in April 1789.
And he strenuously defended it later
against the meter. Though his figure is often presented
as conservative, for his opposition to the meter,
we have to admit that Lalande was quite right in proposing to
base the unit of length on a physical standard, like the
Paris toise, rather than on the size of Earth.
This is exactly what happened
one century later, when in 1889, having metrologists realized that
a practical unit based on Earth
was not accurately reproducible as required for precision measurements
and, most important, the definition itself was basically flawed,
as we shall see at the end of this paper.
The definition of the unit of length
was then solely based upon the platinum standard,
with no reference to Earth any more.
Perhaps what Lalande underestimated was the
psychological driving force of standards taken from nature
that, with all the problems he correctly spotted
(see Ref. [10]), was crucial to reach, soon or later,
some national and international agreement.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... destroyed.8
- It is a matter of fact that
ancient standards are lost forever and the interpretation
of data taken with those units can only be guessed somehow.
A relative recent episode of an important set of
standards lost by accident is the fire in
the British Houses of Parliament in 1834 (see e.g.
[11]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...naturally 9
- The adjective `natural' has been
quite misused in the context of choosing the fundamental
unit of length, calling natural what seems absolutely arbitrary to
others, as we shall see in the sequel.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scale10
- It is not by chance that the
smallest historical unit of time with proper name
is approximately of the order of magnitude of the
human heart pace.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... solution.11
- This choice is not surprising.
Try to build yourself a 25 cm and a 100 cm pendula with
a piece of string and a little weight,
and you do not need to be an great experimenter to
realize that, if you want to use one of them to define
a unit length, you would prefer to work with the longer one.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Jefferson12
- Jefferson
states to have read the Talleyrand's report to the National
Academy of France when his report was practically ready.
Yet the ``proposition made by the Bishop of Autun'' -- this
way Talleyrand was known -- convinced him
to change the reference latitude of the pendulum from
38
 , ``medium latitude of the United States'',
to
, ``medium latitude of the United States'',
to 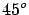 [22].
[22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... preferred.13
- A homogeneous rod of length
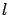 oscillating from one end behaves as a simple pendulum of length
oscillating from one end behaves as a simple pendulum of length 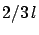 .
Therefore Jefferson's second bar was 3/2 the seconds pendulum,
i.e. about 150 cm.
.
Therefore Jefferson's second bar was 3/2 the seconds pendulum,
i.e. about 150 cm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Miller14
- Indeed, there
were contacts
between Talleyrand and Miller to collaborate towards a common
solution. But due to technical and political events,
the most relevant among them being certainly
the French choice of the meridian,
the projects based on the pendula were put aside in France, Great Britain
and United States between 1790 and 1791, as we shall see later.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... States.15
- Jefferson
had already accepted the French proposal of the
45th parallel, because ``middle term between the equator
and both poles, and a term which consequently might unite the nations
of both hemispheres, appeared to me well chosen, and so just
that I did not hesitate a moment to prefer it
to that of
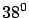 '' [22].
'' [22].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
commission,16
- The Commission was made up of Jean Charles Borda,
Condorcet, Joseph Louis Lagrange,
Pierre Simon de Laplace and Mathieu Tillet.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... scale17
- Historians generally agree
that Mouton attempted the first metric system in 1670 when
he proposed that all distances should be measured by
means of a decimal system of units [25].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... commission18
- This commission was made up of Borda,
Lagrange, Laplace, Gaspar Monge and Condorcet. They worked
in close contact with Antoine Laurent Lavoisier[26].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... determined.19
- Any person can easily
determine the length of a seconds pendulum within the percent level.
Surveying the Earth is a problem more difficult by orders of magnitude.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1852 m.20
- The unit of speed consistent with it
is the knot, corresponding to 1 nautical mile per hour.
It is particularly suited in navigation (and hence the name).
For example, a ship that sails at 30 nodes along a meridian
travels one degree in latitude in two hours.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
commission.21
- The Mouton's minute of meridian is just one of
the possible subdivision of the meridian, namely the 324000-th part
of the quarter of the meridian: we understand that the subdivision
of the right angle in 90 degrees and each degree in 60 minutes and 60 seconds
was judged `unnatural' by the académiciens
because not decimal. We might guess that
the radius of Earth was not considered for the `obvious
difficulty' to make an
immediate measurement from the center of Earth to its surface.
However, it should be similarly obvious that
it was also impossible to measure
all other quantities (diameter, meridian, equator)
in an immediate way. We shall come back to this point
in section 7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
measure22
- The difficulty in measuring arcs of the equator
is not only related to perform measurements in central
Africa or South America.
It would have required precise measurements of differences in longitude
along the equator, and measurements of longitude are intrinsically much
more difficult than measurements of latitude, because the former
rely on absolute synchronizations of clocks in different places,
and that was not an easy task at that time.
(For a novelized account of those
difficulties, see Dava Sobel's Longitude [28].
A classical novel in which practical ways to
measure latitude and longitude are well
described is Jules Vernes's Mysterious Island.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... democratic'.23
- Several of the claims
and the slogans of the académiciens show a certain
degree of naïveness (frankly a bit too much
for such extraordinary clever people they were:
the suspicion that they had
hidden purposes in mind is almost unavoidable).
We shall come back to this point in section 7.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lengths''.24
- Actually,
such a length is not
`precisely' the average over the lengths at all parallels, but
only a very good approximation. In fact, the net
gravitation acceleration
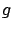 does not vary linearly with the
latitude, but follows the following law [24]:
does not vary linearly with the
latitude, but follows the following law [24]:
where 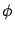 is the latitude (the theoretical formula
is valid at the ellipsoid surface and, as is customary in geodesy,
is the latitude (the theoretical formula
is valid at the ellipsoid surface and, as is customary in geodesy,
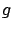 is the sum of the effects of
gravitation and centrifugal forces).
is the sum of the effects of
gravitation and centrifugal forces).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
day.25
- Ten billion is the square of one hundred thousand
(the length of the pendulum is proportional
to the square of its period).
Seen with modern eyes, it looks a bit bizarre
that this `hypothetical pendulum', sized almost
twenty times the distance Earth-Moon,
would have been natural, while the second wouldn't.
(By the way, for those who like to understand all digits:
73cm comes from rounding to the pouce a
length that, directly rounded to the centimeter,
would be 74cm.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
pendulum26
- It should be noted that a unit of length based
on the pendulum has intrinsic problems, like the dependence
of its period on temperature, latitude and above sea level,
plus other more technical issues, considered also in Jefferson's
document [22]. But, in the part of the report
in which the seconds pendulum is discussed and rejected
as unit of length, the French commission
does not seem concerned at all with this kind of
physical questions. Only later (p. 9), when they propose the
pendulum as ancillary reference of length, they specify that
the pendulum should beat ``at the sea level, on vacuum and
at the temperature of melting ice.'' [2]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it.27
- Our
note: to be precise, that is not right ``the same thing.''
The pendulum relates space and time via the net gravitational
acceleration
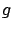 . Therefore the included heterogeneous elements
are two: time and acceleration. A similar situation happens now,
where the meter is related to the second via the speed of light.
. Therefore the included heterogeneous elements
are two: time and acceleration. A similar situation happens now,
where the meter is related to the second via the speed of light.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `meter'28
- The
name `meter' comes from Greek metron, meaning
`measure'. The first who proposed the name
meter in the
context of the French Academy work
is acknowledged to be
the mathematician Leblond in 1790 [30,31];
still, some historians (see e.g. Ref. [29])
maintain the idea has to be originally attributed to Borda.
However, the name meter for a unit of length (that practically
coincides with the French Academy meter) was proposed
more than one century earlier by Burattini
(see Appendix B).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... stadium.29
- Due to uncertainties in
the conversion factor stadium-meter, approximations and errors
in evaluating distances and differences in latitude, the
usually quoted value of 40000 kilometers obtained by Eratosthenes
has to be considered fortuitous, being the uncertainty
on that number of the order of 10% [24]. Anyway,
not bad for that time (in frontier physics a completely new
measurement that provides a result with 10% uncertainty is
considered a good achievement).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
meridian30
- The Paris meridian, now
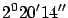 East,
had been the oldest zero longitude, until in 1884
it was replaced by the Greenwich meridian, even though France and Ireland
adopted the new zero only in 1911.
East,
had been the oldest zero longitude, until in 1884
it was replaced by the Greenwich meridian, even though France and Ireland
adopted the new zero only in 1911.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equator.31
- The Lapland
expedition measured
an arc of
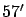 crossing the north polar circle in northen Finland,
at an average latitude of
crossing the north polar circle in northen Finland,
at an average latitude of
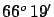 N.
The Peru expedition measured an arc of
N.
The Peru expedition measured an arc of
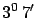 at an average latitude of
at an average latitude of
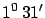 S
(see [36]
for a nice web site dedicated to the expeditions).
S
(see [36]
for a nice web site dedicated to the expeditions).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Perpignan,32
- More precisely, the
lowest latitude was about Collioure,
a small town close to the
Spanish border.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... flattening.33
- The
Dunkerque-Barcelona arc is sufficiently large to allow an
estimate of the meridian curvatures in several sub-arcs and to make an
independent estimate of Earth flattening. That came out to be
about one half of that based on many data sets
from equator to Lapland. The flattening based on the
latter information was finally preferred,
As Alder puts it ``...1/150 offered the best description
of the arc as it passed through France, but they knew that the
older data offered a more plausible picture of the overall
curve of the Earth. They could choose consistency or plausibility.
And after some heated discussion, they chose plausibility
and the old data.'' Actually, the discrepancy between the
values of flattening in different sub-arcs
was a first indication that Earth has
a more complicate shape than just a rotational ellipsoid,
giving rise to the concept of Geoid (see e.g. [24]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... meridian.34
-
We would like to point out that the two results would come
to a better agreement if they were treated in the same way.
In fact, correction for flattening was not applied to the
Lacaille-Cassini result.
In Table 3 we have done the exercise of
calculating the length of the meridian from
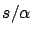 of
Delambre-Méchain, equal to 57019 toises/degree. We obtain
a resulting meter of
443.379 lines. Since the Lacaille-Cassini arc was roughly
similar to the Delambre-Méchain one, we can use the ratio
443.296/443.379 as an
approximate correction factor to take into account
Earth flattening in the Lacaille-Cassini data.
After the correction the meridian length becomes
40006 km and the corrected provisional meter would be 443.36 lignes
(and
of
Delambre-Méchain, equal to 57019 toises/degree. We obtain
a resulting meter of
443.379 lines. Since the Lacaille-Cassini arc was roughly
similar to the Delambre-Méchain one, we can use the ratio
443.296/443.379 as an
approximate correction factor to take into account
Earth flattening in the Lacaille-Cassini data.
After the correction the meridian length becomes
40006 km and the corrected provisional meter would be 443.36 lignes
(and 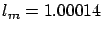 m), i.e. a difference of
only 0.064 lignes (1.4 mm)
with respect to the 1799 final meter.
Anyway, though the two results get closer, the one
based on the Lacaille-Cassini measurements gets also
slightly closer to the present value of the meridian length.
m), i.e. a difference of
only 0.064 lignes (1.4 mm)
with respect to the 1799 final meter.
Anyway, though the two results get closer, the one
based on the Lacaille-Cassini measurements gets also
slightly closer to the present value of the meridian length.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
number.35
- The task specified in the
4th point was later
committed to Borda and Charles Augustin de Coulomb.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... pendulum36
- This name is not
appropriate for the pendulum mentioned in
the 1791 document, as the name 'meter' had still to be
made official. Nevertheless, let us call it so hereafter.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... measurement:37
- That could be the reason
why the world best selling encyclopedia erroneously reports
that the meter
``was originally defined as one ten-millionth of the
distance from the equator to the North Pole
on a line running through Paris.''[44]
This could be just a minor flaw due to superficiality,
but it could also be a heritage of the anglo-saxon
reaction to what was perceived as a French imposition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... problems.38
- As a side remark, we would like
to point out that even the very interesting Alder's book
The Measure of All Things [10], that has been very useful
to us in this research, is a proof the dreams of
the académiciens are still far from coming true. In fact
most lengths are given in feet and inches,
used by to American and British readers,
but hard for the others, especially when, in translation, unavoidable
mistakes happen, as the 25 feet of page 188, that becomes 672 meters
at page 289 of the Italian edition. Nothing compared to the
Mars Climate Orbiter disaster, but this is symptomatic
of the troubles that disuniformity of units of measures still causes,
made worse by globalization.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Earth.39
- This remains true also if an elliptic,
rather than spherical model, is considered, though two
parameters have to be taken into account, instead then just one.
One might argue that the meridian has the advantage that
it is bound only to the assumed rotational symmetry of Earth,
and not to its particular shape (sphere, ellipse,
or even something more complicate). But, apart from the fact
the second commission report [2] speaks explicitly
of measuring an arc of meridian, this possibility would imply
to envisage a campaign of triangulation from the pole to the equator,
that would have been infeasible at that time.
(Remember that before 1909 the north pole
was just an hypothetical place never reached by human beings.)
As a matter of fact, the preferred parameters of
modern geodesy to characterize
the Earth ellipsoid (also called `spheroid')
are the equatorial radius and the flattening. In particular, the latter
is the best determined Earth parameter, given with 12 significant digits
(the value of table 4
has been rounded):
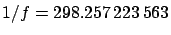 (WGS84)[24,46].
(WGS84)[24,46].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time,40
- With
this respect, a
suggestion put forward in 1889 by
Max Planck has been particularly influential.
He proposed that systems of units should be based on values
assigned conventionally to certain fundamental physical constants.
The first (partial) realization of Planck's idea took place in 1983
when the constancy of the speed of light in different
inertial frames, adopted by Albert Einstein as the grounding principle
of special relativity,
was finally used to relate the unit of length
to the unit of time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
mission.41
- ``The new measures are being adopted
for the commerce independent of the new measure of the earth;
so there is little need for you to push yourself too hard
to bring your result now'', wrote Lalande to Delambre
(cited in Ref. [10]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... unique.42
- Even not taking into account asperities
of the ground, hills and mountains,
the concept of spheroid (or solenoid),
is just a first approximation of the Earth shape (the 'zero-th order'
approximation is the sphere). The equipotential surface of
Earth has a complicate shape called Geoid, of which the spheroid
is a kind of best fitting curve (see e.g. Ref.[46]
for an introduction, that also contains a visual representation
of the Geoid).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... length.43
- That is due neither to ``le difficoltà
ad applicare tale definizione, causate dalla forma
sferica della terra'' (the difficulties to apply such
a definition, caused by the spherical shape of the
Earth) [47], nor because
``later it was discovered that the Earth is
not a perfect sphere''[44].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
meridian.44
- One might also think of a simplification
due to the fact the length of the pendulum is unitary.
To readers with little
physics background we would like to make clear
that what matters
for the pendulum period
is the length, and not the unit in which the length is expressed.
The value of a generic quantity
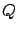 is given by
is given by
![$Q=\{Q\}\cdot [Q]$](img108.png) ,
where
,
where ![$[Q]$](img109.png) is the unit of measurement and
is the unit of measurement and
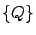 the numerical value,
e.g.
the numerical value,
e.g. 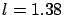 m.
If we change unit of measurement from system
m.
If we change unit of measurement from system 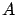 to
system
to
system 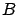 ,
,
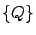 and
and ![$[Q]$](img109.png) change, preserving
change, preserving 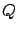 invariant:
invariant:
The two numerical values are then related by
If we call M a different unit of length, such that
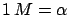 m, we get
m, we get
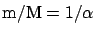 .
Therefore, a length
.
Therefore, a length 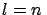 m will be
expressed
as
m will be
expressed
as
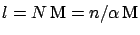 in the new unit
(but the length is the same: you will not grow up,
if your height is expressed in centimeters or millimeters
rather than in meters).
As far as Eq. (1) is concerned,
the numerical value of
in the new unit
(but the length is the same: you will not grow up,
if your height is expressed in centimeters or millimeters
rather than in meters).
As far as Eq. (1) is concerned,
the numerical value of 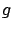 will be transformed in the same way as
will be transformed in the same way as 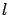 ,
namely
,
namely
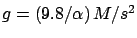 . As a consequence, the conversion factor
. As a consequence, the conversion factor
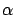 simplifies in Eq. (1) and the period will remain
the same, as it must be.
simplifies in Eq. (1) and the period will remain
the same, as it must be.
On the other hand, if we consider a different length,
that has unitary numerical value in the new unit M,
we get a different
period of the pendulum,
namely
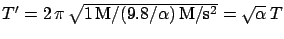 .
(For example, if the new unit of length
is twice the meter, the half period of a simple pendulum
of unitary length will be 1.419s).
.
(For example, if the new unit of length
is twice the meter, the half period of a simple pendulum
of unitary length will be 1.419s).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
radius45
- The generic `radius of Earth'
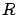 refers usually to the equatorial radius and it implies
that Earth is considered sufficiently spherical for
the purpose of the calculations.
refers usually to the equatorial radius and it implies
that Earth is considered sufficiently spherical for
the purpose of the calculations.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rotation.46
- At the equator, the negative centrifugal acceleration
gives a contribution to
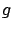 equal to
equal to
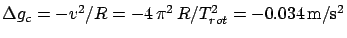 (
(
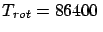 s stands for the rotation period).
Note that, however, in geodesy `gravitational acceleration'
s stands for the rotation period).
Note that, however, in geodesy `gravitational acceleration' 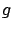 indicates the overall free fall acceleration experienced by a body
and takes into account the genuine gravitational force and
the centrifugal one.
indicates the overall free fall acceleration experienced by a body
and takes into account the genuine gravitational force and
the centrifugal one.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
century,47
- Tito Livio Burattini (born 1617 in Agordo,
Belluno, Italy
and died 1681 in Krakow, Poland)
was an Italian Egyptologist, inventor, architect,
scientist, instrument-maker, and traveler.
He was an extremely versatile person
(he even designed ``flying machines''!), with interests in mathematics,
physics, astronomy, geodesy and economics. He spent a few years in Egypt,
where he prepared a triangulation map of this country
(he was also an excellent cartographer),
made measurements of many pyramids and obelisks,
copied monuments and tried to classify them. After
some stay in Germany, he finally settled in Krakow, where
he served as the King's architect. There he
performed optical experiments and contributed to the discovery
of irregularities on the surface of Venus,
in collaboration with the astronomers Stanislaw
Pudlowsky, a former student of Galileo, and Girolamo Pinocci.
He became also a highly regarded maker of microscope and
telescope lenses, sending some of them as gifts to Cardinal
Leopold de' Medici. In 1645, he published Bilancia
Sincera, where he proposed an improvement to the
hydrostatic balance described by Galileo in his Bilancetta.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... WORLD.'' 48
- ``Trattato nel qual si mostra come in tutti
li Luoghi del Mondo si può trovare una MISURA, & un PESO UNIVERSALE
senza che habbiano relazione con niun'altra MISURA, e niun altro PESO,
& ad ogni modo in tutti li luoghi saranno li medesimi,
e saranno inalterabili,
e perpetui sin tanto che durerà il MONDO.''
(The original is for the pleasure of Italian readers.)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... it.'' 49
- ``Dunque
li Pendoli
saranno la base dell'opera mia, e da quelli cavarò prima il mio
Metro Cattolico, cioè misura universale, che così mi pare di
nominarla in lingua Greca, e poi da questa cavarò un Peso Cattolico.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Clocks. 50
- ``Il Metro
Cattolico
non è altro che la lunghezza di un Pendolo, le di cui vibrazioni
siano 3600 in un hora [...]
ch'io intendo d'un Pendolo libero,
e non di quelli che sono attaccati agli Horologi.''
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.