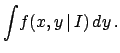Introduction

A common task in data analysis is to `determine', on the basis of experimental observations, the values of the parameters of a model that relates physical quantities. This procedure is usually associated to names like `fit' and `regression', and to principles, like 'least squares' or `maximum likelihood' (with variants). I prefer, as many others belonging to a still small minority, to approach the problem from more fundamental probabilistic `first principles', that are indeed the fundamental rules of probability theory. This approach is also called `Bayesian' because of the central role played by Bayes' theorem in the process of learning from data, as we shall see in a while (for a critical introduction to the Bayesian approach see Ref. [2] and references therein). In practice this means that we rank in probability hypotheses and numerical values about which we are not certain. This is rather intuitive and it is indeed the natural way physicists reason (see e.g. Ref. [3] and references therein), though we have been taught a peculiar view of probability that does not allow us to make the reasonings we intuitively do and that we are going to use here.

In the so called Bayesian approach the issue of `fits' takes the name of parametric inference, in the sense we are interested in inferring the parameters of a model that relates `true' values. The outcome of the inference is an uncertain knowledge of parameters, whose possible values are ranked using the language and the tools of probability theory. As it can only be (see e.g. Ref. [2] for extensive discussions), the resulting inference depends on the inferential model and on previous knowledge about the possible values the model parameters can take (though this last dependence is usually rather weak if the inference is based on a `large' number of observations). It is then important to state clearly the several assumptions that enter the data analysis. I hope this paper does it with the due care - and I apologize in advance for some pedantry and repetitions. The main message I would like to convey is that nowadays it is much more important to build up the model that describes at best the physics case than to obtain simple formulae for the 'best estimates' and their uncertainty. This is because, thanks to the extraordinary progresses of applied mathematics and computing power, in most cases the calculation of the integrals that come from a straight application of the probability theory does not require any longer titanic efforts. Building up the correct model is then equivalent, in most cases, to have solved the problem.

The paper is organized as follows. In Section 2 the inferential approach is introduced from scratch, only assuming the multivariate extensions of the following well known formulas¹

$$f(x,y\,\vert\,I) = f(x\,\vert\,y,I)\cdot f(y\,\vert\,I)$$ (1)

$$f(x\,\vert\,I) = \int\!f(x,y\,\vert\,I)\,dy\,.$$ (2)

We show how to build the general model, and how this evolves as soon as the several hypotheses of the model are introduced (independence, normal error functions, linear dependence between true values, vague priors). The graphical representation of the model in terms of the so called `Bayesian networks' is also shown, the utility of which will become self-evident. The case of linear fit with errors on both axes is then summarized in Section 3, and the approximate solution for the non-linear case is sketched in Section 4. The extra variability of the data is modeled in Section 5, first in general and then in the simple case of the linear fit. The interpretation of the inferential result is discussed in Section 6, in which approximated methods to calculate the fit summaries (expected values and variance of the parameters) are shown. Finally, some comments on the not-trivial issues related to the use of linear fit formulas to infer the parameters of exponential and power laws are given in Section 7. Section 8 shows how to extend the model to include systematic errors, and some simple formulas to take into account offset and scale systematic errors in the case of linear fits will be provided. The paper ends with some conclusions and some comments about the debate that has triggered it.