


Next: Approximated solution for non-linear
Up: Fits, and especially linear
Previous: Probabilistic parametric inference from
Linear fit with normal errors on both axes
To apply the general formulas of the previous section
we only need to make explicit
 and the error functions, and finally
integrate over
and the error functions, and finally
integrate over 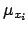 .
In the case of linear fit with normal errors
the individual contributions
to the likelihoods become
.
In the case of linear fit with normal errors
the individual contributions
to the likelihoods become
that, inserted into Eq. (25), finally give
The effect of the error of the 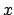 -values is to have an effective
standard error on the
-values is to have an effective
standard error on the 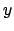 -values that is the quadratic combination
of
-values that is the quadratic combination
of 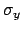 and
and 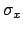 , the latter `propagated'
to the other coordinate via the slope
, the latter `propagated'
to the other coordinate via the slope 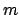 (this result can be justified heuristically by dimensional analysis).
(this result can be justified heuristically by dimensional analysis).



Next: Approximated solution for non-linear
Up: Fits, and especially linear
Previous: Probabilistic parametric inference from
Giulio D'Agostini
2005-11-21
![$\displaystyle k_{x_i}
\int \frac{1}{\sqrt{2\pi}\, \sigma_{x_i}}\,
\exp{ \left[ ...
...\frac{(y_i-m\,\mu_{x_i}-c)^2}
{2\,\sigma_{y_i}^2}
\right]
} \,\, d{\mu_{x_i}}\,$](img103.png)
![$\displaystyle k_{x_i} \, \frac{1}{\sqrt{2\pi}\, \sqrt{\sigma_{y_i}^2+m^2\,\sigm...
...\frac{(y_i-m\,x_i-c)^2}
{2\, (\sigma_{y_i}^2+m^2\,\sigma_{x_i}^2) }
\right]}\,,$](img104.png)