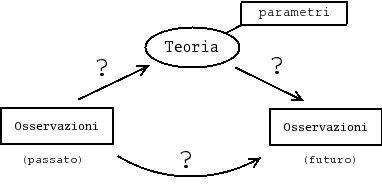
Mi piace rappresentare l'attività del `fisico' con il seguente diagramma. (Nel seguito mi riferirò spesso alla `Fisica', ma solo per bias personale e perché essa è comunemente percepita come la Scienza della Natura per antonomasia, essendo il carattere delle argomentazioni che seguiranno del tutto generale.)

Ma una Scienza non è una semplice lista di fatti.
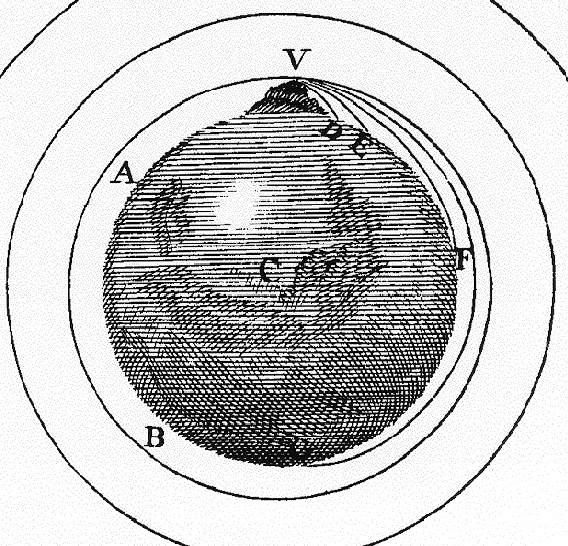
Come è ben noto, il passaggio dalle osservazioni alla teoria non è affatto automatico. Da sempre l'uomo ha visto `mele' cadere e la luna errare nel cielo, ma bisognava attendere Newton per capire che sono due aspetti dello stesso fenomeno, come perfettamente illustrato nella famosa figura dei Principia Matematica (opera contenente, fra l'altro, le leges motus):
Vediamo ora il ruolo dei punti interrogativi del diagramma iniziale. Essi rappresentano incertezza: siamo in condizioni di incertezza sulle teorie e/o sui loro parametri; siamo in condizioni di incertezza su quanto misureremo nelle osservazioni future.
Cominciamo dalla freccia a destra, che in un certo è quella più importante e rende conto anche di quella a sinistra. L'incertezza di previsione può essere dovuta a diverse ragioni.
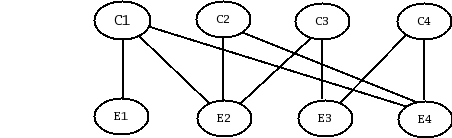
Per esempio, e questo è il toy model da me preferito, invece di una sola scatola con 3 palline bianche e 2 nere, si può pensare alle 6 possibili scatole contenenti 5 palline, che chiamiamo H0, H1, ..., H5, dove l'indice indica il numero di palline bianche e il simbolo H sta a ricordare che sono le ipotesi in gioco.

Prendiamo una scatola a caso ed estraiamo una pallina. Esce bianco (B). Quale scatola avevamo preso? Possiamo reintrodurre la pallina, agitare e andare avanti con l'esperimento. I dati sperimentali (la sequenza osservata) modificano a mano a mano la nostra opinione sulla scatola misteriosa. Di consequenza cambieranno anche le nostre aspettative sul tipo di pallina che andremo ad estrarre.
È chiara l'analogia con il processo di misura. A causa degli inevitabili errori di misura, un valore vero (μ) non produce in modo univoco un valore osservato (x). Quindi, avendo osservato x non siamo certi sul valore di μ.
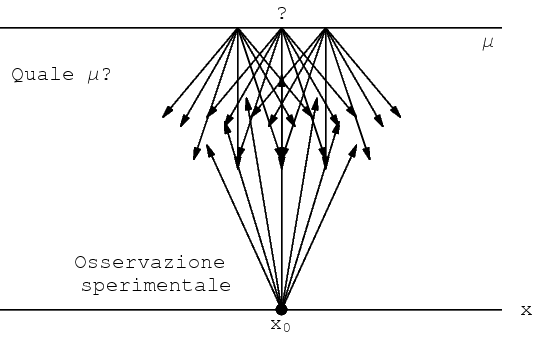
Il fatto che l'indice con il quale identifichiamo le scatole sia un intero nell'intervallo [0,5], mentre a μ si associa generalmente una variabile continua, non cambia la natura del problema. Ne risulta invece decisamente semplificata la comprensione del processo mentale attraverso il quale aggiorniamo le nostre opinioni sia sulle teorie e i loro parametri, sia sulle future osservazioni.
Abbiamo quindi ricondotto l'apprendimento dall'esperienza a quello che Poincaré chiamava in Scienza e Ipotesi un “problema nella probabilità delle cause” e che sosteneva essere “il problema essenziale del metodo sperimentale”.
È curioso constatare come in genere si insegni
per poco, male o per niente a risolvere
problemi del genere, riconosciuti
come essenziali da oltre un secolo e che richiedono una matematica
assolutamente elementare - nel caso discreto non serve più
dell'aritmetica!
[Chi scrive sta tenendo in questi mesi un corso di
Probabilità
e Incertezza di Misura
al dottorato in Fisica della Sapienza e sembra incredibile
che, dei quasi venti brillantissimi giovani, nessuno era inizialmente
in grado di affrontare in modo quantitativo il problema
delle sei scatole, che è diventato quindi il motivo
conduttore di una parte del corso. Similmente, della decina
di studenti di matematica che seguivano inizialmente il
corso di
Preparazione di Esperienze Didattiche, nessuno era in grado di risolvere
semplici problemi pratici della probabilità delle cause,
pur avendo seguito nella triennale almeno un corso di probabilità.]
Quello dell'insegnamento del ragionamento probabilistico, con un approccio che lo renda applicabile ad una grande varietà di problemi, sembra un problema antico, del quale, si lamentava già Leibnitz tre secoli fa, come ci ricorda Hume che così scriveva a metà del '700 nell'Estratto di un Trattato della Natura Umana: “The celebrated Monsieur Leibniz has observed it to be a defect in the common systems of logic, that they are very copious when they explain the operations of the understanding in the forming of demonstrations, but are too concise when they treat of probabilities, and those other measures of evidence on which life and action entirely depend, and which are our guides even in most of our philosophical speculations”.
Riprendiamo il nostro esperimento didattico (non virtuale, in quanto, anzi, si presta molto bene ad essere eseguito e discusso anche in una classe di liceo) delle sei scatole. È molto facile valutare la probabilità degli effetti, ovvero di P(Ej|Hi), ove E1=B, bianco, e E2=N, nero:
| P(Ej|Hi) | ||||||
|---|---|---|---|---|---|---|
| Pallina | Scatola | |||||
| H0 | H1 | H2 | H3 | H4 | H5 | |
| E1=B | 0 | 1/5 | 2/5 | 3/5 | 4/5 | 1 |
| E2=N | 1 | 4/5 | 3/5 | 2/5 | 1/5 | 0 |
Inizialmente P(Hi) vale 1/6 per ogni i, mentre P(Ej) vale 1/2 per ogni j, data la simmetria del problema, e la formula di Bayes ci fornisce i valori di probabilità P(Hi|B) modificati dal dato sperimentale. In particolare, P(H0|B)=0, ovvero l'ipotesi `tutte nere' viene `falsificata' in quanto essa non può generare l'effetto `pallina bianca' (il falsificazionismo viene prontamente recuperato nella cosidetta statistica Bayesiana come caso particolare), mentre la nostra credenza nelle altre scatole diventa proporzionale al numero di palline bianche (e su questo l'approccio sì/no del falsificazionismo non dice nulla!).
Come si capisce bene, la probabilità di una pallina bianca ad una eventuale seconda estrazione (previo reimbussolamento) aumenta, in quanto, pur restando costante la risposta del rivelatore [questa è l'illuminante rilettura di P(Ej|Hi) per la successive applicazioni nella trattazione delle incertezze di misura], il peso delle ipotesi è ora sbilanciato verso grandi i [infatti la formula generale che dà la probabilità di bianco o nero tenendo conto di tutte le ipotesi in gioco, ovvero P(Ej)=ΣiP(Ej|Hi)×P(Hi), è proprio una media pesata, in quanto ΣiP(Hi)=1].
Il resto del `giochino' è riportato in un numero speciale dell'American Journal of Physics, disponibile anche nell'arXiv in forma di preprint. Nell'articolo vengono anche discussi diversi aspetti dell'insegnamento della probabilità nei corsi di Laurea in Fisica (con ricadute anche nell'insegnamento secondario) e, come sottolinea il titolo, il ruolo chiarificatore e unificatore dell'approccio soggettivo.
Il passaggio a valori incerti continui è anche discusso nell'articolo, con ovvia applicazione al caso delle misure, ovvero come ricavare f(μ|x) a partire da f(x|μ), dove f() sta per la `funzione di densità di probabilità';, nel caso elementare di distribuzione `normale', ovvero gaussiana, degli errori.
Per altre applicazioni, inclusa risposta del rivelatore non gaussiana (di fondamentale importanza sono quelle binomiali e poissoniane, che giocano un ruolo essenziale nelle misure di conteggio), trattazione delle incertezze dovute ad errori sistematici, propagazione di incertezze, fit e molto altro (ma sempre con un approccio consistente, basato sulla teoria della probabilità, invece delle usuali formulette ad hoc) si può consultare l'abbondante materiale nel sito dell'autore, in particolare nella pagina dedicata all'insegnamento e a quella dedicata a probabilità e statistica.