Principia
Moving finally to the content of the ASA statement,
after a short introduction, in which it is recognized
that ``the p-value 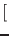 ...
...![$]$](img29.png) is commonly misused
and misinterpreted,''
and a reminder of what a p-value
``informally''' is (``the probability under a specified
statistical model that a statistical summary of the data
is commonly misused
and misinterpreted,''
and a reminder of what a p-value
``informally''' is (``the probability under a specified
statistical model that a statistical summary of the data
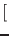 ...
...![$]$](img29.png) would be equal
to or more extreme than its observed value'') a list
of six items, indicated as ``principles'', follows
(the highlighting is original).
would be equal
to or more extreme than its observed value'') a list
of six items, indicated as ``principles'', follows
(the highlighting is original).
- P-values can indicate how incompatible the data are
with a specified statistical model.
A  -value provides one approach to summarizing
the incompatibility between a particular set of data and
a proposed model for the data. The most common
context is a model, constructed under a set of assumptions,
together with a so-called ``null hypothesis.'' Often
the null hypothesis postulates the absence of an effect,
such as no difference between two groups, or the absence
of a relationship between a factor and an outcome. The
smaller the
-value provides one approach to summarizing
the incompatibility between a particular set of data and
a proposed model for the data. The most common
context is a model, constructed under a set of assumptions,
together with a so-called ``null hypothesis.'' Often
the null hypothesis postulates the absence of an effect,
such as no difference between two groups, or the absence
of a relationship between a factor and an outcome. The
smaller the  -value, the greater the statistical
incompatibility of the data with the null hypothesis,
if the underlying assumptions used to calculate the
-value, the greater the statistical
incompatibility of the data with the null hypothesis,
if the underlying assumptions used to calculate the  -value hold. This
incompatibility can be interpreted as casting doubt on
or providing evidence against the null hypothesis or the
underlying assumptions.
-value hold. This
incompatibility can be interpreted as casting doubt on
or providing evidence against the null hypothesis or the
underlying assumptions.
- P-values do not measure the probability
that the studied hypothesis is true, or the probability that the data
were produced by random chance alone.
Researchers often
wish to turn a  -value into a statement about the truth of a null hypothesis,
or about the probability that random chance produced the observed
data. The
-value into a statement about the truth of a null hypothesis,
or about the probability that random chance produced the observed
data. The  -value is neither. It is a statement about data
in relation to a specified hypothetical explanation, and is
not a statement about the explanation itself.
-value is neither. It is a statement about data
in relation to a specified hypothetical explanation, and is
not a statement about the explanation itself.
- Scientific conclusions and business or policy decisions
should not be based only on whether a p-value passes
a specific threshold.
Practices
that reduce data analysis or scientific inference to mechanical
``bright-line'' rules
(such as ``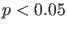 '') for justifying scientific
claims or conclusions can
lead to erroneous beliefs and poor decision making. A
conclusion does not immediately become ``true'' on one
side of the divide and ``false'' on the other. Researchers
should bring many contextual factors into play to derive
scientific inferences, including the design of a study,
the quality of the measurements, the external evidence
for the phenomenon under study, and the validity of
assumptions that underlie the data analysis. Pragmatic
considerations often require binary, ``yes-no'' decisions,
but this does not mean that
'') for justifying scientific
claims or conclusions can
lead to erroneous beliefs and poor decision making. A
conclusion does not immediately become ``true'' on one
side of the divide and ``false'' on the other. Researchers
should bring many contextual factors into play to derive
scientific inferences, including the design of a study,
the quality of the measurements, the external evidence
for the phenomenon under study, and the validity of
assumptions that underlie the data analysis. Pragmatic
considerations often require binary, ``yes-no'' decisions,
but this does not mean that  -values alone can ensure
that a decision is correct or incorrect. The widespread
use of ``statistical significance'' (generally interpreted as
-values alone can ensure
that a decision is correct or incorrect. The widespread
use of ``statistical significance'' (generally interpreted as
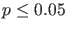 '') as a license for making a claim of a scientific
finding (or implied truth) leads to considerable distortion
of the scientific process.
'') as a license for making a claim of a scientific
finding (or implied truth) leads to considerable distortion
of the scientific process.
- Proper inference requires full reporting and transparency
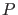 -values and related analyses
should not be reported selectively. Conducting multiple analyses of the data
and reporting only those with certain
-values and related analyses
should not be reported selectively. Conducting multiple analyses of the data
and reporting only those with certain  -values
(typically those passing a significance threshold) renders the
reported
-values
(typically those passing a significance threshold) renders the
reported  -values essentially uninterpretable. Cherry-picking
promising findings, also known by such terms as
data dredging, significance chasing, significance questing,
selective inference, and ``
-values essentially uninterpretable. Cherry-picking
promising findings, also known by such terms as
data dredging, significance chasing, significance questing,
selective inference, and `` -hacking,'' leads to a
spurious excess of statistically significant results in the
published literature and should be vigorously avoided.
One need not formally carry out multiple statistical tests
for this problem to arise: Whenever a researcher chooses
what to present based on statistical results, valid
interpretation of those results is severely compromised if
the reader is not informed of the choice and its basis.
Researchers should disclose the number of hypotheses
explored during the study, all data collection decisions,
all statistical analyses conducted, and all
-hacking,'' leads to a
spurious excess of statistically significant results in the
published literature and should be vigorously avoided.
One need not formally carry out multiple statistical tests
for this problem to arise: Whenever a researcher chooses
what to present based on statistical results, valid
interpretation of those results is severely compromised if
the reader is not informed of the choice and its basis.
Researchers should disclose the number of hypotheses
explored during the study, all data collection decisions,
all statistical analyses conducted, and all  -values computed.
Valid scientific conclusions based on
-values computed.
Valid scientific conclusions based on  -values and
related statistics cannot be drawn without at least knowing
how many and which analyses were conducted, and
how those analyses (including
-values and
related statistics cannot be drawn without at least knowing
how many and which analyses were conducted, and
how those analyses (including  -values) were selected for
reporting.
-values) were selected for
reporting.
- A p-value, or statistical significance, does not measure
the size of an effect or the importance of a result.
Statistical
significance is not equivalent to scientific,
human, or economic significance. Smaller  -values
do not necessarily imply the presence of larger or
more important effects, and larger
-values
do not necessarily imply the presence of larger or
more important effects, and larger  -values do not
imply a lack of importance or even lack of effect. Any
effect, no matter how tiny, can produce a small
-values do not
imply a lack of importance or even lack of effect. Any
effect, no matter how tiny, can produce a small  -value
if the sample size or measurement precision is high
enough, and large effects may produce unimpressive
-value
if the sample size or measurement precision is high
enough, and large effects may produce unimpressive
 -values if the sample size is small or measurements
are imprecise. Similarly, identical estimated effects will
have different
-values if the sample size is small or measurements
are imprecise. Similarly, identical estimated effects will
have different  -values if the precision of the estimates
differs.
-values if the precision of the estimates
differs.
- By itself, a p-value does not provide a good measure of
evidence regarding a model or hypothesis.
Researchers should recognize
that a  -value without
context or other evidence provides limited information.
For example, a
-value without
context or other evidence provides limited information.
For example, a  -value near 0.05 taken by itself offers only
weak evidence against the null hypothesis. Likewise, a
relatively large
-value near 0.05 taken by itself offers only
weak evidence against the null hypothesis. Likewise, a
relatively large  -value does not imply evidence in favor
of the null hypothesis; many other hypotheses may be
equally or more consistent with the observed data. For
these reasons, data analysis should not end with the calculation
of a
-value does not imply evidence in favor
of the null hypothesis; many other hypotheses may be
equally or more consistent with the observed data. For
these reasons, data analysis should not end with the calculation
of a  -value when other approaches are appropriate and feasible.
-value when other approaches are appropriate and feasible.
These words sound as an admission of failure
of much of the statistics teaching and practice
in the past many decades.
But yet I find their courageous statement still
somehow unsatisfactory, and, in particular,
the first principle is in my opinion
still affected by the kind of `original sin'
at the basis of p-value misinterpretations and misuse.
Many practitioners consider in fact a value occurring several
(but often just a few)
standard deviations from the `expected value' (in the probabilistic
sense) to be a 'deviance' from the model, which is clearly
absurd: no value a model can yield can be considered an
exception from the model itself
(see also footnote 11 -
the reason why ``p-values often work''
will be discussed in section 6).
Then, moving to principle 2,
it is not that ``researchers often wish to turn a  -value
into a statement about the truth of a null hypothesis''
(italic mine),
as if this would be an extravagant fantasy: reasoning
in terms of degree of belief of whatever is uncertain
is connatural to the
`human understanding'[46]:
all methods that do not tackle straight the fundamental
issue of the probability of hypotheses,
in the problems in which this is the crucial question,
are destinated to fail, and to perpetuate misunderstanding
and misuse.
-value
into a statement about the truth of a null hypothesis''
(italic mine),
as if this would be an extravagant fantasy: reasoning
in terms of degree of belief of whatever is uncertain
is connatural to the
`human understanding'[46]:
all methods that do not tackle straight the fundamental
issue of the probability of hypotheses,
in the problems in which this is the crucial question,
are destinated to fail, and to perpetuate misunderstanding
and misuse.
Giulio D'Agostini
2016-09-06