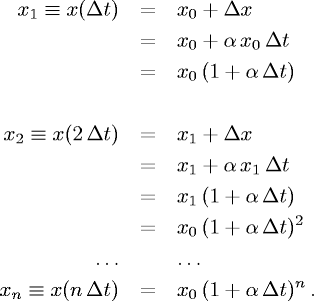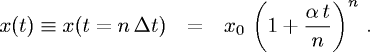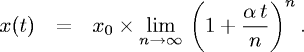Appunti per la lezione nr. 13 (4 aprile)
Immaginiamo che la variaxione nel tempo della variabile 'x' sia caratterizzata da

-> la variazione relativa ('percentuale') della variabile 'x' è
proporzionale all'intervallo di tempo.
Possiamo riscrivere la stessa equazione come
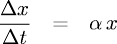
-> il tasso di crescita/decrescita (a seconda del segno di α) della variabile 'x' è
proporzionale al valore della variabile.
Si tratta ora di capire come varia x con il tempo.
Cominciamo a vedere cosa succede
dopo Δt, dopo 2Δt, etc., partendo dal valore x0 all'istante t=0:
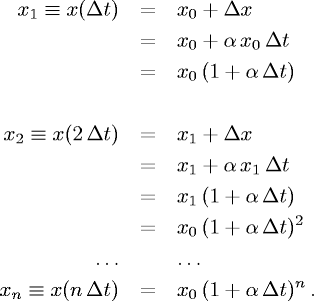
↠ Progressione geometrica di ragione (1+α·Δt),
maggiore o minore di 1 a seconda del segno di α.
Dopo un tempo t = nΔt si ha quindi
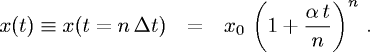
Immaginiamo di 'affettare' ora il tempo t in tantissimi intervallini Δt.
Al limite, il numero di intervallini diventa infinito e la loro ampiezza nulla.
Si tratta di trovare quindi il limite
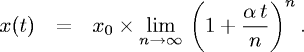
Cerchiamo di capire quanto vale questo limite in modo 'pratico', non rigoroso,
analizzando la seguente tabella compilata con αt=1 e αt=-1:
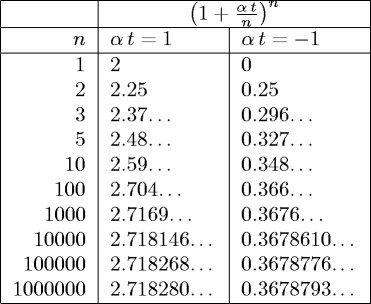
Come si può verificare facilmente, il limite converge a eαt,
ove e è la costante di Eulero, base dei logaritmi naturali
(in effetti, vedi bibliografia, una delle definizioni di e è proprio
legata a questo limite).
In conclusione, la soluzione cercata è
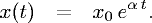
Inoltre
- essa può riscritta, a seconda del segno di α, come x(t)=x0 e t/τ
o come x(t)=x0 e -t/τ, ove τ=1/|α|;
- da τ (o da α) si ricavano, come facile esercizio,
il tempo di raddoppio o di dimezzamento.
Bibliografia su limite a esponenziale:
- Costante e di Eulero: vedi
qui
o qui
(quest'ultimo soprattutto per l'equivalenza fra le due definizioni più note).