• 24 novembre (18:09-18:13; el. max 31°; Mag -2.5);
• 25 novembre (17:21-17:28; el. max 44°; Mag -3.2);
• 27 novembre (17:24-17:29; el. max 22°; Mag -2.2).

[ Dai Principia di Newton ]

[ da La Fisica di Feynman]

Il cosiddetto 'cannone di Newton' è un esperimento concettuale per far capire che le mele che cascano e la luna che gira derivano dalle stessi leggi della Fisica.

• Un'animazione a rallentatore (su piccole distanze).
• Simulazione interattiva con possibilità di scegliere la velocità iniziale.

Semplici concetti di Matematica e Fisica

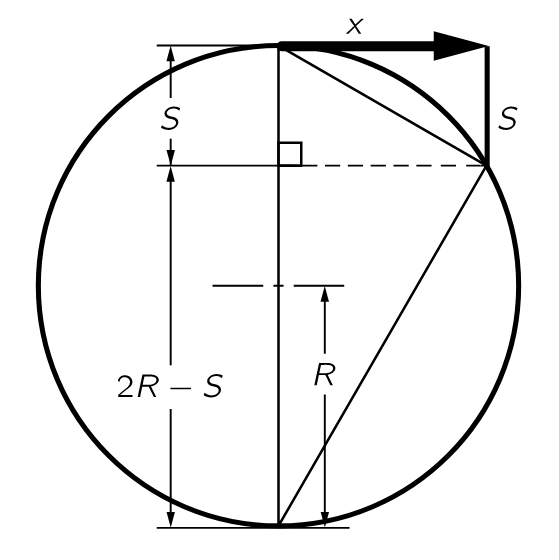
• Secondo teorema di Euclide.
• Teorema di Talete relativo a triangoli inscritti in una semicirconferenza.
• Spazio percorso da un corpo in caduta libera: s = 1/2 g t²:
  → spazio di caduta libera nel primo secondo: 4.9 m.
• Legge di gravità: F = G M m / R².
  (Raggio terrestre: c.a 6.4×10³ km).
• Forza peso in prossimità della superficie terrestre: F = G M_T m / R² = 'm g' (trascurando alcuni effetti);
• Accelerazione centripeta in un moto circolare uniforme: a = v²/R.

Satelliti intorno alla Terra

• Confronto dei vari parametri;
• Movimento rispetto alla Terra dei satelliti geostazionari

Slides introduttive aspettando l'ISS

• ISSflaswob.pdf

• 2020-11-23-Note-18-26.pdf (assolutamente non rieditata)
• Supplemento (in risposta a domanda arrivata dopo il flaswob): supplemento_lavagna.pdf:
  • fa capire il confronto dei vari parametri dei satelliti orbitanti intorno alla Terra;
  • → terza legge di Keplero (seppur dimostrata nel caso particolare di orbite circolari),
    da cui si può calcolare facilmente, ad es., T_Luna/T_ISS, etc.
• Altra domanda ricevuta dopo due settimane: "ma allora la stazione orbitale, non risentendo di attriti, seguiterà a orbitare all'infinito?"
  • R: Purtroppo no. Anche si trova a oltre 400 km dalla superficie terrestre, qualche piccolo attrito ce l'ha e perde costantemente quota, qualcosa dell'ordine di una quindicina di metri al giorno. Quindi ogni tanto ha bisogno di una `spintarella' verso l'alto che le faccia riguadagnare quota:
    • Grafico della quota durante il 2020
    • Sito con grafico aggiornato
    • Caso di Tiangong, caduta all'inizio del 2018, in quanto ne era stato perso il controllo: altezza dal 2011 al 2018

• Gli antichi Greci: la misura della distanza della Luna;
• Ombra della Terra sulla Luna:provare a emulare Aristarco di Samo per valutare il rapporto fra grandezza della Luna e grandezza della Terra.