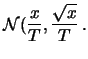Next: Caso binomiale
Up: Inferenza su e (o
Previous: Inferenza su e (o
Indice
Se il numero di conteggi osservato è grande, la verosimiglianza
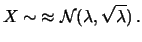 è pressoché gaussiana, ovvero
Se si assume una condizione sufficiente vaga su
è pressoché gaussiana, ovvero
Se si assume una condizione sufficiente vaga su 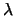 si
ha
con
si
ha
con
ovvero
A seconda che i conteggi siano nel dominio del tempo o dello spazio
si possono inferire le opportune intensità dei processi di Poisson
associati dividendo per il tempo o la porzione di spazio nel
quale si sono verificati i conteggi. Ad esempio, se i conteggi si sono
verificati in un tempo 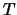 perfettamente noto, abbiamo
perfettamente noto, abbiamo




Next: Caso binomiale
Up: Inferenza su e (o
Previous: Inferenza su e (o
Indice
Giulio D'Agostini
2001-04-02