



Next: Formule dei minimi quadrati
Up: Adattamento di curve ai
Previous: Inferenza sui parametri di
Indice
Per affrontare il problema dal punto di vista piu' generale possibile,
si noti come la (15.2) permette di fare una inferenza
su tutte le grandezze incerte (in numero di 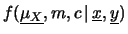 , con
, con  pari al numero di
punti sperimentali), ovvero:
pari al numero di
punti sperimentali), ovvero:
Assumendo una distribuzione uniforme
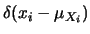 ,
abbiamo che
,
abbiamo che
- se
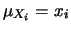 allora le gaussiane che descrivono
la probabilità di
allora le gaussiane che descrivono
la probabilità di  intorno a
intorno a 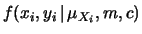 diventano delle
diventano delle
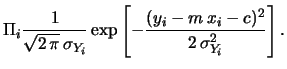 e quindi
e quindi
- Il caso generale di
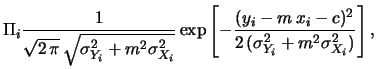 può essere trattato
esattamente nello stesso modo, con la complicazione che l'integrale
è un po' più complicato. Il risultato è
può essere trattato
esattamente nello stesso modo, con la complicazione che l'integrale
è un po' più complicato. Il risultato è
che si riconduce al caso precedente quando
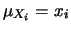 .
Essenzialmente essa dice che si sostituiscono alle
.
Essenzialmente essa dice che si sostituiscono alle
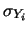 delle deviazioni standard effettive ottentue sommando in quadratura
quelle delle
delle deviazioni standard effettive ottentue sommando in quadratura
quelle delle  e quelle delle
e quelle delle  , opportunamente propagate mediante
la derivata
, opportunamente propagate mediante
la derivata
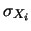 , che nel caso lineare
è esattamente
, che nel caso lineare
è esattamente 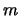 . Ovviamente, in questo caso la soluzione
diventa più complicata, ma il problema può essere affrontato
per iterazione, calcolando
. Ovviamente, in questo caso la soluzione
diventa più complicata, ma il problema può essere affrontato
per iterazione, calcolando 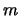 e
e 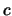 senza tener conto delle
senza tener conto delle
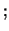 e poi inserendo nelle formule le deviazioni
standard effettive calcolate con questo valore di
e poi inserendo nelle formule le deviazioni
standard effettive calcolate con questo valore di 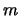 . La
convergenza è, in genere talmente rapida, che, se
i punti sono già stati graficati, nemmeno vale
la pena di fare troppi conti: basta valutare a occhio
. La
convergenza è, in genere talmente rapida, che, se
i punti sono già stati graficati, nemmeno vale
la pena di fare troppi conti: basta valutare a occhio 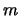 dal
grafico e usare questo valore nel calcolo delle deviazioni
standard effettive.
dal
grafico e usare questo valore nel calcolo delle deviazioni
standard effettive.




Next: Formule dei minimi quadrati
Up: Adattamento di curve ai
Previous: Inferenza sui parametri di
Indice
Giulio D'Agostini
2001-04-02
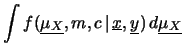
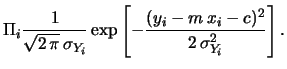 e quindi
e quindi
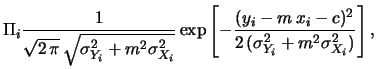 può essere trattato
esattamente nello stesso modo, con la complicazione che l'integrale
è un po' più complicato. Il risultato è
può essere trattato
esattamente nello stesso modo, con la complicazione che l'integrale
è un po' più complicato. Il risultato è