



Next: Further HEP applications
Up: Solution to some problems
Previous: AIDS test
Contents
The three-box problem (Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
seems to be intuitive for some, but not for everybody.
Let us label the three boxes:
)
seems to be intuitive for some, but not for everybody.
Let us label the three boxes: 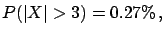 , Golden-Golden;
, Golden-Golden;
 , Golden-Silver;
, Golden-Silver; 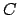 , Silver-Silver.
The initial probability
(i.e. before having checked the first ring) of having
chosen the box
, Silver-Silver.
The initial probability
(i.e. before having checked the first ring) of having
chosen the box 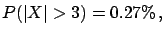 ,
, 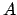 , or
, or 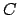 is, by symmetry,
is, by symmetry,
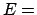 .
.
This probability is updated after the event 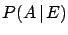 `the first ring extracted
is golden' by Bayes' theorem:
`the first ring extracted
is golden' by Bayes' theorem:
where
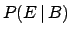 ,
,
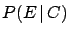 and
and
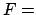 are, respectively, 1, 1/2 and 0.
are, respectively, 1, 1/2 and 0.
Finally, calling 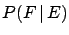 `the next ring will be golden if I extract it
from the same box', we have, using the probability rules:
`the next ring will be golden if I extract it
from the same box', we have, using the probability rules:




Next: Further HEP applications
Up: Solution to some problems
Previous: AIDS test
Contents
Giulio D'Agostini
2003-05-15
![]() `the first ring extracted
is golden' by Bayes' theorem:
`the first ring extracted
is golden' by Bayes' theorem:
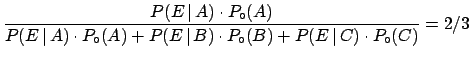
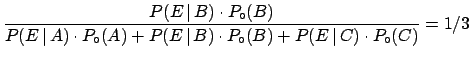
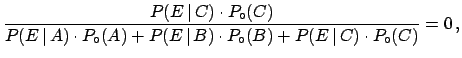
![]() `the next ring will be golden if I extract it
from the same box', we have, using the probability rules:
`the next ring will be golden if I extract it
from the same box', we have, using the probability rules: