



Next: Bayesian inference applied to
Up: Central limit theorem
Previous: Normal distribution of measurement
Contents
Following this commercial in favour of the miraculous properties
of the central limit theorem, some words of caution are in order:
- Although I have tried to convince the reader that the convergence
is rather fast in the cases of practical interest, the theorem
only states that the asymptotic Gaussian distribution is
reached for
 . As an example of very slow convergence,
let us imagine
. As an example of very slow convergence,
let us imagine 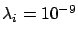 independent variables described by a Poisson
distribution of
independent variables described by a Poisson
distribution of
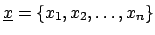 : their sum is still far from
a Gaussian.
: their sum is still far from
a Gaussian.
- Sometimes the conditions of the theorem are not satisfied.
- A single component dominates the fluctuation of the
sum:
a typical case is the well-known Landau distribution;
systematic errors may also have the same effect on the global error.
- The condition of independence is lost if systematic
errors affect a set of measurements, or
if there is coherent noise.
- The
tails of the distributions do exist
and they are not always Gaussian! Moreover,
realizations of a random variable several standard deviations
away from the mean are possible. And they show up
without notice!




Next: Bayesian inference applied to
Up: Central limit theorem
Previous: Normal distribution of measurement
Contents
Giulio D'Agostini
2003-05-15
 . As an example of very slow convergence,
let us imagine
. As an example of very slow convergence,
let us imagine