



Next: Normally distributed observables
Up: Choice of the initial
Previous: Difference with respect to
Contents
A good example to help understand the problems outlined
in the previous section
is the so-called Bertrand paradox.
- Problem:
- Given a circle of radius
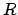 and a chord drawn randomly on it,
what is the probability that the length
and a chord drawn randomly on it,
what is the probability that the length 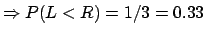 of the chord
is smaller than
of the chord
is smaller than
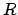 ?
?
- Solution 1:
- Choose ``randomly'' two points on the circumference
and draw a chord between them:
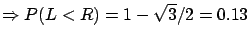 .
.
- Solution 2:
- Choose a straight line passing through
the centre
of the circle; then draw a second line, orthogonal to the first,
and which intersects it inside the circle at a
``random'' distance from the center:
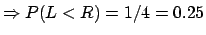 .
.
- Solution 3:
- Choose ``randomly'' a point inside the circle and
draw a straight line orthogonal to the radius
that passes through
the chosen point
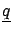 .
.
- Your solution:
 ?
?
- Question:
- What is the origin of the paradox?
- Answer:
- The problem does not specify how to ``randomly''
choose the chord. The three solutions take a
uniform distribution:
along the circumference; along the the radius; inside
the circle. What is uniform in one variable is not uniform in the others!
- Question:
- Which is the right solution?
In principle you may imagine an infinite number of different solutions.
From a physicist's viewpoint
any attempt to answer this question is a waste of time.
The reason why the paradox
has been compared to the Byzantine discussions
about the sex of angels is that there are indeed people arguing
about it. For example, there is a school of thought which
insists that Solution 2 is the right one.
In fact this kind of paradox, together with abuse of the Indifference
Principle for problems like ``what is the probability that the
sun will rise tomorrow morning'' threw a shadow over
Bayesian methods at the end of the last century. The maximum likelihood
method, which does not make explicit use of prior distributions,
was then seen as a valid solution to the problem. But
in reality
the ambiguity of the proper metrics on which
the initial distribution is uniform has an equivalent
in the arbitrariness of the variable used in the likelihood function.
In the end, what was criticized
when it was stated explicitly in the Bayes formula is
accepted passively when it is hidden in the maximum
likelihood method.




Next: Normally distributed observables
Up: Choice of the initial
Previous: Difference with respect to
Contents
Giulio D'Agostini
2003-05-15