



Next: Probability of observables versus
Up: Uncertainty in physics and
Previous: Sources of measurement uncertainty
Contents
The present situation
concerning the treatment of
measurement uncertainties can be
summarized as follows.
- Uncertainties due to statistical errors are currently
treated using the frequentistic concept
of `confidence interval', although
- there are well known cases -- of great relevance in
frontier
physics -- in which the approach is not applicable
(e.g. small number of observed events, or measurement
close to the edge of the physical region);
- the procedure is rather unnatural, and in fact the interpretation
of the results is unconsciously subjective (as will be discussed later).
- There is no satisfactory theory or model to treat
uncertainties due to systematic errors1.3 consistently. Only ad hoc prescriptions can be
found in the literature and in practice
(``my supervisor says ...''): ``add them linearly'';
``add them linearly if ..., else add them quadratically'';
``don't add them at all''.1.4 The fashion at the moment is to add them quadratically
if they are considered to be independent, or to build a
covariance matrix of statistical and systematic contribution
to treat the general case. In my opinion,
besides all the theoretically motivated excuses for justifying this praxis,
there is simply
the reluctance of experimentalists to combine linearly
10, 20 or more contributions to a global uncertainty,
as the (out of fashion) `theory' of maximum bounds
would require.1.5
The problem of interpretation will be treated in the next section.
For the moment, let us see why the use of standard propagation
of uncertainty, namely
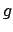 |
(1.1) |
is not justified (especially if contributions due
to systematic effects are included).
This formula is derived from the rules of
probability distributions,
making use of linearization (a usually reasonable approximation
for routine applications). This leads to theoretical
and practical problems.
 and
and 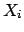 should have the meaning of random variables.
should have the meaning of random variables.
- In the case of systematic effects,
how do we evaluate the input quantities
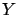 entering in the formula
in a way which is consistent with their
meaning as standard deviations?
entering in the formula
in a way which is consistent with their
meaning as standard deviations?
- How do we properly take into account correlations (assuming we have
solved the previous questions)?
It is very interesting to go to your favourite textbook
and see how `error propagation' is introduced. You will realize
that some formulae are developed
for random quantities, making use of linear approximations,
and then suddenly they are used for physics quantities
without any justification.1.6A typical example is measuring a velocity
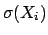 from
a distance
from
a distance
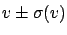 and a time interval
and a time interval
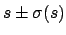 .
It is really a challenge to go from
the uncertainty on
.
It is really a challenge to go from
the uncertainty on 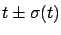 and
and 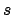 to that of
to that of 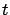 without
considering
without
considering 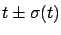 ,
, 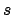 and
and 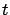 as random variables, and to avoid
thinking of the final result as
a probabilistic statement on the velocity.
Also in this case, an intuitive interpretation conflicts
with standard probability
theory.
as random variables, and to avoid
thinking of the final result as
a probabilistic statement on the velocity.
Also in this case, an intuitive interpretation conflicts
with standard probability
theory.




Next: Probability of observables versus
Up: Uncertainty in physics and
Previous: Sources of measurement uncertainty
Contents
Giulio D'Agostini
2003-05-15
 and
and