



Next: Offset uncertainty
Up: Use and misuse of
Previous: Use and misuse of
Contents
Once the covariance matrix is built
one uses it in a 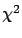 fit to get the
parameters of a function.
The quantity to be minimized is
fit to get the
parameters of a function.
The quantity to be minimized is
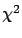 , defined as
, defined as
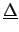 |
(6.47) |
where
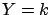 is the vector of the differences
between the theoretical and the experimental values.
Let us
consider the simple case in which two results of the same physical quantity
are available, and the individual and the common
standard uncertainty are known.
The best estimate of the true value of the physical quantity
is then obtained by fitting the constant
is the vector of the differences
between the theoretical and the experimental values.
Let us
consider the simple case in which two results of the same physical quantity
are available, and the individual and the common
standard uncertainty are known.
The best estimate of the true value of the physical quantity
is then obtained by fitting the constant
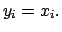 through the data points. In this simple case
the
through the data points. In this simple case
the 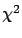 minimization can be performed easily.
We will consider
the two cases of offset and normalization uncertainty. As before,
we assume that the detector is well calibrated, i.e. the most
probable value of the calibration constant is, respectively
for the two cases, 0 and 1, and hence
minimization can be performed easily.
We will consider
the two cases of offset and normalization uncertainty. As before,
we assume that the detector is well calibrated, i.e. the most
probable value of the calibration constant is, respectively
for the two cases, 0 and 1, and hence 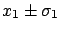




Next: Offset uncertainty
Up: Use and misuse of
Previous: Use and misuse of
Contents
Giulio D'Agostini
2003-05-15