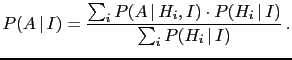Other important rules

Important relations that follow from the basic rules are ($A$ is also a generic hypothesis):

$$P(\overline H\,\vert\,I) = 1 - P(H\,\vert\,I)$$ (29)

$$P(H\cap \overline H\,\vert\,I) =$$ 0 (30)

$$P(H_i\cup H_j\,\vert\,I) = P(H_i\,\vert\,I) + P(H_j\,\vert\,I) - P(H_i\cap H_j\,\vert\,I)$$ (31)

$$P(A\,\vert\,I) = P(A\cap H\,\vert\,I) + P(A\cap \overline H\,\vert\,I)$$ (32)

$$= P(A\,\vert\,H,I)\cdot P(H\,\vert\,I) + P(A\,\vert\,\overline H,I) \cdot P(\overline H\,\vert\,I)$$ (33)

$$P(A\,\vert\,I) = \sum_i P(A\cap H_i\,\vert\,I) \hspace{0.5cm}( \mbox{if $H_i$\ form a {\it complete class}} )$$ (34)

$$= \sum_i P(A\,\vert\,H_i,I)\cdot P(H_i\,\vert\,I) \hspace{0.5cm}( )\,.$$ (35)

The first two rules are quite obvious. Eq. (31) is an extension of the third basic rule in the case two hypotheses are not mutually exclusive. In fact, if this is not case, the probability of $H_i\cap H_j$ is double counted and needs to be subtracted. Eq. (32) is also very intuitive, because either $A$ is true together with $H$ or with its opposite.

Formally, Eq. (33) follows from Eq. (32) and basic rule 4. Its interpretation is that the probability of any hypothesis can be seen as `weighted average' of conditional probabilities, with weights given by the probabilities of the conditionands [remember that $P(H\,\vert\,I)+P(\overline H\,\vert\,I)=1$ and therefore Eq. (33) can be rewritten as

$$P(A\,\vert\,I)= \frac{P(A\,\vert\,H,I)\cdot P(H\,\vert\,I) + P(A\... ...) \cdot P(\overline H\,\vert\,I)}{P(H\,\vert\,I)+P(\overline H\,\vert\,I)}\,,$$

that makes self evident its weighted average interpretation].

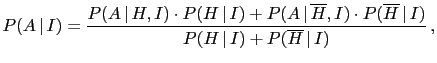
Eq. (34) and (35) are simple extensions of Eq. (32) and (33) to a generic `complete class', defined as a set of mutually exclusive hypotheses [ $H_i\cap H_j=\emptyset$, i.e. $P(H_i\cap H_j\,\vert\,I)=0$], of which at least one must be true [ $\cup_iH_i=\Omega$, i.e. $\sum_i P(H_i\,\vert\,I)=1$]. It follows then that Eq. (35) can be rewritten as the (`more explicit') weighted average

$$P(A\,\vert\,I)= \frac{\sum_i P(A\,\vert\,H_i,I)\cdot P(H_i\,\vert\,I)} {\sum_i P(H_i\,\vert\,I)}\,.$$

[Note that any hypothesis $H$ and its opposite $\overline H$ form a complete class, because $P(H\cap \overline H\,\vert\,I)=0$ and $P(H\cup \overline H\,\vert\,I)=1$.]