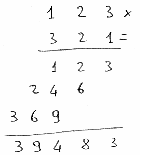Recentemente fa i media passavano la notizia, accompagnata da video illustrativi,² di un cosidetto metodo giapponese per eseguire moltiplicazioni a mano senza far uso delle tabelline.³ ”Addio tabelline” titolavano addirittura siti vari, anche di testate influenti [1], nei quali le notizie vengono troppo spesso ’ripostate’ in modo acritico. I facili esempi numerici potevano indurre ingenui internauti a credere che in un breve futuro si potesse fare a meno delle tabelline per eseguire moltiplicazioni a mano. È quanto manifesta una ragazza con grande entusiasmo al padre, episodio dal quale prendono spunto i dialoghi qui riportati, i quali pur non essendo reali, sono verosimili, essendo Maddalena la figlia dell’autore. Ovviamente la valenza rivoluzionaria del nuovo metodo viene facilmente smontata, mentre ne viene messa in luce la sua utilità didattica per mostrare, o ricordare, i ragionamenti sui quali si basa il metodo appreso alle elementari ed eseguito per lo più meccanicamente.

F.

Guarda che figo, papà!

P.

Qualche impresa da Guinness? O nuovo modello di…

F.

No, no, stavolta è roba seria, e ti interesserà di sicuro!

P.

Una novità che possa interessare sia a te che a me? “O fatto proprio strano da giocarci al lotto…” Non succedeva da quando usciva un nuovo gioco della Wii.

F.

In effetti è quasi un gioco.

P.

Aspetta un istante che invio questo mail e…

F.

Questa mail, papà. Mail è femminile. Lo ha detto pure…

P.

Senti, Maddale’, io mando mail da più di trent’anni e me ne frego di quello che ha decretato qualche sapientone.

F.

Ma ‘posta’ è femminile…

F.

E infatti io non mando ‘una posta’, bensì un messaggio, e forse è per questo che nella mia mente ‘mail’ è maschile. E infatti, nel mio ambiente si diceva “an e-mail message”. Comunque, ecco, un momento,…e-mail sent, così hai poco da ridire. Allora dimmi, di che si tratta?

F.

Matematica.

P.

Uhm, matematica? E da quand’è che ti eccita?

F.

In genere no, ma questa è troppo forte, anche se per me è troppo tardi, visto che le tabelline oramai le ho dovute imparare.

P.

Hanno tolto le tabelline dai programmi scolastici? Non mi stupirei di niente. Tanto oramai l’interesse primario non è quello di formare i ragazzi, ma di vendere libri e sussidi, …e gite scolastiche, o come diavolo si chiamano oggigiorno… Io alle elementari andavo a scuola con il libro di lettura e il sussidiario, un quaderno a righe e uno a quadretti. Tu avevi uno zainetto che pesava più di te. E alla fine non mi sembra che la conoscenza acquisita sia proporzionale al peso dei libri e dei quaderni che ci siamo portati dietro, o trascinati nei carrelli.

F.

Non ancora abolite, ma sicuramente le aboliranno. Ecco, leggi qua: “Tabelline addio, la moltiplicazione giapponese rende i calcoli un gioco.” E ancora, “Addio tabelline, il metodo giapponese rivoluziona i calcoli.”

P.

Perbacco! E come funziona?

F.

Ecco, guarda, ho visto il video e ti faccio vedere come si fa 21 per 23.

P.

483, giusto?

F.

Con te non c’è gusto. Hai fatto prima dei giapponesi. Ma come hai fatto?

P.

Non ci vuole molto. 20 volte 23 fa 460, a cui devi aggiungere una volta 23. I numeri sono facili e non ci sono riporti.

F.

Sì, ma così devi pensare!

P.

Ah ah ah, dimenticavo, voi siete quelli che vorreste non pensare, tanto c’è qualcuno che pensa per voi. Uhm, francamente non mi sembra una bella pensata la vostra.

F.

No, non è così…

P.

Va be’, lasciamo stare le discussioni sui ‘massimi sistemi’ e veniamo al problema specifico. Allora, cosa fanno i giapponesi, invece di pensare?

F.

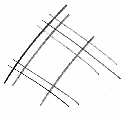
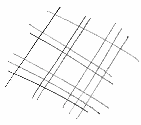
Guarda, disegno su un foglio due linee parallele per il primo ‘2’, poi, ben distanziata, un’altra linea parallela che sta per ‘1’. E le faccio inclinate di 45 gradi, poi vedrai perché.

P.

Perché no? Anche se la notazione mi sembra decisamente regressiva rispetto a quella escogitata dagli arabi o chi per loro. E direi che non è neppure ecosostenibile, come si dice oggi per essere alla moda, visto per scrivere 21 hai consumato un quarto di foglio. Ma vai avanti.

F.

Ora ci traccio sopra le linee che indicano 23, ma a 90 gradi rispetto a quelle del 21, ecco, così.

P.

Interessante!

F.

Mi prendi in giro?

P.

No, lo sto dicendo sul serio. Ma vai avanti, mi sembra di aver capito.

F.

Certo che hai capito, sicuramente. Io invece so come arrivare al risultato ma non ho ancora capito bene perché. Ora ti faccio vedere.

P.

In effetti il risultato è già lì, in forma grafica, e va solo letto opportunamente.

F.

Ecco, vediamo le linee dei ‘2’…

P.

Quelle delle decine…

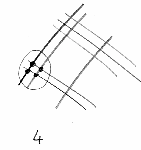
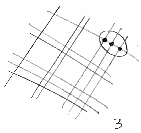
F.

…che si intersecano in quattro punti, e scriviamo ‘4’.

Poi ci sono le linee che indicano ‘1’ e ‘3’…

P.

Quelle delle unità…

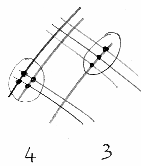
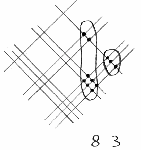
F.

…che hanno solo tre punti di intersezione, e scriviamo ‘3’.

E infine le altre intersezioni: le due linee della prima decina – giusto? – che incontrano le tre linee delle unità di ‘23’, e le due linee della seconda decina con la linea della prima unità. In totale fanno otto intersezioni

P.

Simpatico, anche se non direi efficiente, visto il tempo che ci hai messo e le risorse che hai dovuto impiegare, intendo carta e inchiostro.

F.

Esagerato! Ma la cosa importante è che non ho dovuto pensare…insomma solo un po’ per ricordare la regola, e, soprattutto, non mi è servito sapere le tabelline.

P.

In effetti! Ma questa moltiplicazione era talmente facile che non fa testo. E se le cose si complicano? Per esempio se hai numeri a più di due cifre o…

F.

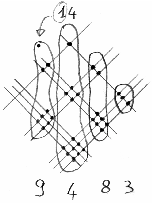
Ecco, ora ti faccio vedere l’altra che c’era sul video. Si tratta di due numeri a 3 cifre, 123 per 321.

P.

Già, fammi vedere.

F.

Di nuovo, una linea, poi due linee e poi ancora tre linee. Ecco, così:

E abbiamo scritto il primo numero.
Poi, a 90 gradi rispetto alle prime, tre linee, seguite da due e poi da una:

E ora ci siamo. Basta solo contare il numero di intersezioni.

P.

Buon divertimento!

F.

In effetti è un divertimento!

P.

Sarà, ma non se devi fare dei conti in tempi rapidi, per qualcosa che ti serve. Ma vai avanti, ti voglio vedere all’opera, visto che il gioco ti diverte.

F.

Per prima cosa contiamo le intersezioni sulla destra, che sono tre.

P.

Ok.

F.

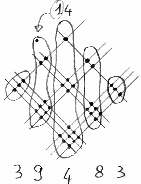
Poi sommiamo tutte le intersezioni allineate a sinistra di queste tre, …uhm, aspetta, mi sto confondendo, fammi rifare bene la figura, perché mi sono persa gli allineamenti.

P.

Ah, andiamo bene…e la moltiplicazione è ancora facile

P.

Dai, papà, sei tu che mi fai emozionare. Aspetta, vado a prendere il righello. Ecco, in questa si capisce meglio.

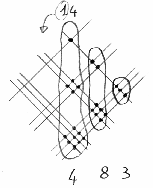
Ho due intersezioni sopra e sei sotto, per un totale di otto. Poi ho, andando a sinistra, una intersezione in alto, quattro al centro e nove in basso, per un totale di 14.

P.

Scusa, come hai fatto a capire che le intersezioni al centro sono quattro?

F.

Si vedono!

P.

E che quelle in basso sono nove?

F.

Beh, tre per tre nove!

P.

E questo è il metodo che evitava l’uso delle tabelline?

F.

In effetti avrei potuto contare i puntini.

P.

Giusto! Anche quando calcoli che quattro volte cinque fa venti puoi contare portando alle labbra, in successione, la punta di ciascun dito della mano sinistra, e usando le dita della mano destra per ricordarti quante volte lo hai fatto. Ma vai avanti.

F.

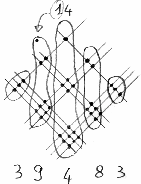
Quindi, dicevo, 14. Scrivo allora ‘4’ e mi ricordo di ’1’, che devo sommare alle intersezioni a sinistra di queste.

Ecco, ce ne sono due sopra e sei sotto e, sommando ’1’ che avanzava prima, otteniamo ’9’.

P.

Brava!

F.

E infine rimangono le tre intersezioni a sinistra,

quindi finalmente…

P.

Già, finalmente…

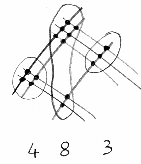
F.

Non essere polemico, papà. Insomma, abbiamo ottenuto, nell’ordine ‘3’, ‘9’, ‘4’, ‘8’ e ‘3’, ovvero 39483.

P.

Il risultato è corretto, bene. Queste erano le moltiplicazioni del video, giusto?

F.

Sì, e ti confesso che prima di fartele vedere mi ero già allenata un paio di volte.

P.

Te ne posso proporre una io?

F.

See, immagino! Conoscendoti, sarà come minimo 345679 per 874005, o qualcosa del genere…

P.

Non esageriamo, facciamo semplicemente 67 per 85. La sapresti fare anche a mano, giusto?

F.

Ci mancherebbe! Alle elementari, con la maestra Stefania, facevamo cose ben più complicate.

P.

Ma sapevi già le tabelline. Ora prova a farla con il metodo dei giapponesi – hai detto che si chiama così, giusto? – e soprattutto senza usare le tabelline.

F.

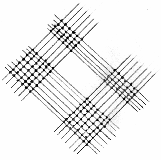
Facile, sei linee per il ‘6’, …, ma stavolta le faccio subito con il righello, …eccole tutte

P.

Bello! Bel motivo per una tovaglia, o anche per una sciarpa, questione di gusti. Risultato?

F.

Allora, cominciamo…innanzitutto 35 intersezioni a destra.

P.

Come fai a saperlo?

F.

Sette per cinque trentacinque.

P.

Avevi detto senza tabelline! Conta!

F.

See, mi sembra la barzelletta “zitto e nuota!”

P.

Ti ci sei messa tu nei pasticci, veramente ora zitta e conta!

F.

Ma contare zitta non ci riesco!

P.

Va be’, basta che conti.

F.

Uno, due, tre, …

P.

A due a due, niente, eh?

F.

Va be’, ricomincio. Due, quattro, sei,…, trentadue, trentaquattro, e uno trentacinque. E fortuna che già sapevo quanto doveva fare, se no vatti a fidare…
Quindi scrivo ‘5’ e mi segno il ‘3’ da riportare a sinistra.

P.

Segna, segna e non ti sbagliare.

F.

Ora ci sono le intersezioni centrali. Ma sono un’infinità!

P.

Non esageriamo!

F.

Sono sei per cinque sopra e otto per sette sotto.

P.

Non ragionare come se stessi già usando le tabelline, zitta e conta!

F.

Papà, facciamo una cosa, facciamo finta che abbia contato, ma uso le tabelline, te ne prego! Se no ci metto una vita e devo ricontare i punti almeno due volte per essere sicura di non essermi sbagliata.

P.

Va bene, ma solo perché sei la mia figlia prediletta…

F.

…non essendocene altre…Allora 30 sopra e 56 sotto, che fanno 86 – fin qui ci arrivo, e la maestra Stefania sarebbe fiera di me.
Poi mi devo ricordare dei 3 che avanzavano prima, e siamo arrivati a 89, quindi - finalmeeente! – scrivo ‘9’ e mi segno ‘8’.
E per ultimo, abbiamo otto per sei, che fa 48 e che, con ‘8’ che riportavo, arrivo a 56. Insomma, se non mi sono sbagliata (e per fortuna mi hai risparmiato il supplizio di contare!), il prodotto vale 5695.

P.

Giusto, come posso verificare usando R sul mio pc.

F.

Non c’è gusto! Dovevi verificare con il metodo ‘nostro’.

P.

Non sono mica scemo! Un conto saperlo usare, e capire su cosa si basa, e un conto usarlo sempre per pedanteria o masochismo. Allora, che te ne pare del metodo giapponese che rivoluzionerà l’insegnamento della matematica alle elementari e eviterà alle generazioni future di imparare le tabelline?

F.

Alla fin fine direi che era meglio come avevo imparato dalla maestra Stefania, usando poi in pratica la calcolatrice o quei cosi che usi tu al computer…

P.

…ma cercando di far girare le nostre rotelline quando si tratta di conti con numeri facili, come 20 per 30, o anche 21 per 23.

F.

Quindi altra bufala che gira su internet, come tante altre?

P.

Se viene presentata con i titoli che mi hai mostrato, direi sicuramente di sì. Se invece è un modo per vedere le moltiplicazioni sotto un altro punto di vista, allora la cosa può essere divertente, e anche istruttiva.

F.

Cosa vuoi dire?

P.

Ripartiamo dal tuo 21 per 23. Il primo numero è composto da due decine e da una unità, il secondo da due decine e tre unità. Indicando con u le unità e con d le decine, li possiamo scrivere quindi come (2d + 1u) e (2d + 3u). Quando li moltiplichiamo…

F.

Prodotto di binomi…

P.

Brava, vai avanti tu…

F.

“Che a me vien da ridere”, come dici sempre.

P.

È proprio il caso…

F.

Quindi, nell’ordine, abbiamo, 4d², 6du, 2ud e 3u². Siccome le decine al quadrato sono centinaia, le decine per le unità sono decine, indipendentemente dall’ordine, e le unità al quadrato sono delle unità, otteniamo 4 centinaia, 8 decine e 3 unità, insomma 483. Quindi – vediamo se ho capito – nel caso di moltiplicazioni a due cifre, il metodo giapponese dà una rappresentazione grafica del prodotto di due binomi. E così via per moltiplicazioni a più cifre, giusto?

P.

Giustissimo! E, a proposito, riguardando i tuoi disegni con le linee, quanti raggruppamenti c’erano quando facevi 21 per 23 e 67 per 85?

F.

Quattro: quello a destra, quello a sinistra e i due centrali. Proprio i quattro termini del prodotto di due binomi.

P.

E quando facevi 123 per 321?

F.

Aspetta che riguar…

P,

No, senza guardare, pensa un attimo.

F.

Uno a destra, uno a sinistra, due…

P.

Ti ho chiesto di pensare, non di ricordare…Anzi ti complico il problema, con la speranza di facilitarti la visione di insieme. Se avessi dovuto fare 12345678 per 87654321, insomma il prodotto di due numeri a otto cifre, quanti raggruppamenti avresti avuto?

F.

Aspe’…

P.

Lascia stare quel righello e la matita, e pensa a una scacchiera.

F.

Cambiamo gioco?

P.

No, analizziamo un problema analogo, caratterizzato da una dimensionalità uguale a quella che ci interessa. Insomma, eravamo partiti dal prodotto di due numeri a due cifre e poi siamo passati a quello di due numeri a tre cifre, e ora siamo saltati a otto.

F.

Ah, ecco, dove vuoi arrivare! La scacchiera ha otto righe e otto colonne, per un totale di sessantaquattro caselle, insomma sessantaquattro possibilità, almeno per la regina. Rappresentano quindi tutti gli incroci possibili – papà, li posso chiamare incroci?

P.

Chiamali come ti pare, se hai capito di cosa si tratta.

F.

Quindi – ecco! – il prodotto di due numeri da otto cifre l’uno produce, con il metodo dei giapponesi, sessantaquattro incroci di righe e colonne, cioè sessantaquattro raggruppamenti. Mentre nel caso di numeri a tre cifre ne producono nove, tre per tre. Sì, erano nove, ora che ci penso bene.

P.

E anche con il nostro metodo abbiamo lo stesso numero di ‘raggruppamenti’, per così dire.

F.

Ma nel nostro metodo non ci sono raggruppamenti!

P.

Ah, no? Puoi fare la moltiplicazione 123 per 321 come avevi imparato alle elementari?

F.

Un momento. Allora, uno per tre, uno per due,…; due per tre, due per due, …Ecco, 39483.

P.

E ora metti i due conti uno affianco all’altro, intendo quello nipponico e quello de noantri.

F.

Eccoli.

   

Ma è la stessa cosa! il ‘3’ a destra da solo, poi i ‘2’ e il ‘6’ allineati, che fanno otto, e così via.

P.

Toh, curioso, non ti pare? Ma forse non sarà un caso…

F.

Ma nel caso di 67 per 85 non funziona.

P.

E perché no? La differenza è che quando il numero di intersezioni in ciascun raggruppamento supera 9, noi facciamo i riporti al volo. Prova a fare 67 per 85 con il nostro metodo senza riporti.

F.

Come si fa? Viene un casino.

P.

Basta che metti i risultati del singolo prodotto fra parentesi.

F.

Ecco, va bene così?

P.

Va bene per forza, se non hai sbagliato a fare i conti.

F.

Papà, le tabelline le so ancora!

P.

Bene, ora prova a rivedere il risultato alla luce di quanto abbiamo detto prima.

F.

In effetti, abbiamo di nuovo quattro raggruppamenti. Uno da 35 unità, che è quello a destra in alto, uno da 48 centinaia, che è quello a sinistra in basso e due, rispettivamente da 30 e da 56 decine, che sono i due incolonnati.

P.

Ergo?

F.

Ergo sum…lasciamo stare cosa…Ma stavolta ho finalmente capito! In effetti 35 unità sono cinque unità e tre decine. E scrivo ‘5’. Poi abbiamo 86 più 3 decine, per un totale di 89 decine, ovvero 9 decine e 8 centinaia. Quindi scrivo ‘9’ a sinistra di ‘5’ e vado avanti. Infine abbiamo 48 più 8 centinaia, ossia 56 centinaia. Quindi sei centinaia e cinque migliaia. Insomma 5695. Stesso risultato, e ho pure capito perché e cosa significano le singole cifre, perché, a ripensarci, quel metodo giapponese, come dicono, oltre a essere praticamente inutilizzabile se le cifre sono grandi, è veramente da automi.

P.

E il numero di operazioni da fare?

F.

Lo stesso, perché devi fare una moltiplicazione per ogni raggruppamento, e il numero dei raggruppamenti è pari al prodotto del numero di cifre di ciascun fattore. Infine devi fare le somme dei raggruppamenti delle stesse ‘cose’, insomma delle decine, delle centinaia, e così via, e poi ci sono i riporti. Insomma i conti sono gli stessi.

P.

E con le tabelline come la mettiamo?

F.

Mi sembrano inevitabili, a meno di non usare solo calcolatrici o programmi al computer. Fare a mano il conteggio del numero di intersezioni in ciascun raggruppamento mi sembra una follia, senza contare i disegni, gli allineamenti e la possibilità di sbagliarsi. Ma ora basta perché è dai tempi della maestra Stefania che non facevo tutti questi conti e mi sta scoppiando la testa.

P.

E già, perché dopo le elementari, viene la ‘Terra di mezzo’, che sono le medie, e poi la ‘Grande ubriacatura’ dei licei, mi riferisco ai programmi di matematica, con cose assolutamente inutili o accessorie alle quali si dà la stessa importanza delle poche cose fondamentali che dovrebbero rimanere impresse nella mente. Ma lasciamo stare.

F.

Sì, sì, lasciamo stare…

P.

Aspe’, non ho finito. Ogni tanto una paternale ci vuole, è mio diritto e dovere, no?

F.

Giusto, e io ascolto compìta. Mio dovere.

P.

Volevo dire che mi ha fatto piacere che, giocandoci insieme su questa cosa, ci hai riflettuto un po’, e poi mi sembra che ti sia pure divertita. Perché la paura mia è nei confronti di coloro che non vogliono che pensiate, tanto pensano loro, e non di certo ai vostri interessi. O, in tempi di internet, di quelli che dicono cose senza averci pensato, e pretendono che siccome “siamo in democrazia” la loro opinione valga come quella di chi, coscienziosamente, sulle cose ci ha meditato non poco, e che in fondo, proprio perché intellettualmente onesto, qualche dubbio ce lo può ancora avere. Ignoranza e ostentazione di sicurezza sembra che vadano troppo spesso insieme, di questi tempi. Insomma, e poi ti lascio a quello che stavi facendo, permettimi di leggerti una battuta che mi è arrivata poco fa, per mail, da un amico, pescata non so dove nel mare magnum dei social. Non sono di quelli che detesta o criminalizza questi nuovi mezzi di comunicazione, ma ci vuole un po’, anzi tanta accortezza per non affogarcisi, o bere schifezze, in questo mare. Un momento che la ritrovo. Ecco, “il problema della libertà di pensiero non è l’assenza di libertà, ma l’assenza di PENSIERO.”

References