


Next: Extra variability of the
Up: Fits, and especially linear
Previous: Linear fit with normal
Approximated solution for non-linear fits with normal errors
Linearity implies that the arguments of the exponential
of the integrand in Eq. (28) contains only
first and second powers of 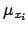 , and then the integrals
has a closed solution. Though this is not true in general,
the linear case teaches us how to get an approximated
solution of the problem. We can take first order expansions
of
, and then the integrals
has a closed solution. Though this is not true in general,
the linear case teaches us how to get an approximated
solution of the problem. We can take first order expansions
of
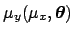 around each
around each 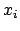
The difference
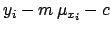 in Eq. (28),
that was indeed equal to
in Eq. (28),
that was indeed equal to
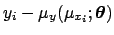 in the general case,
using the linear approximation becomes
in the general case,
using the linear approximation becomes
i.e.
we have the following replacements in Eqs. (28)-(30):
The approximated equivalent of
Eq. (30) is then
where the unusual symbol `
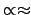 ' stands for
`approximately proportional to'.
' stands for
`approximately proportional to'.



Next: Extra variability of the
Up: Fits, and especially linear
Previous: Linear fit with normal
Giulio D'Agostini
2005-11-21