


Next: Partial results from ,
Up: Inferring and of the
Previous: Introduction
Uncertain constraints
The relations (1)-(4) of Ref. [1] can be written
in the following way
where 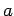 ,
,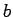 , ...
, ...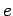 are the constraint parameters, functions
of many quantities; the most crucial of those determined experimentally
are indicated on the left hand side of the equations.
Note that the order of
are the constraint parameters, functions
of many quantities; the most crucial of those determined experimentally
are indicated on the left hand side of the equations.
Note that the order of 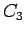 and
and 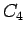 is exchanged with respect to
Eqs. (3)-(4) of Ref. [1]. This is because,
since the present information concerning
is exchanged with respect to
Eqs. (3)-(4) of Ref. [1]. This is because,
since the present information concerning 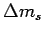 is of different quality with respect to the other quantities,
the constraint
is of different quality with respect to the other quantities,
the constraint 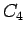 needs a more careful treatment than the others,
and it will be introduced after
needs a more careful treatment than the others,
and it will be introduced after 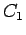 -
-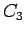 .
This is also the reason why
.
This is also the reason why 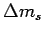 appears explicitly in
the constraint
appears explicitly in
the constraint 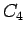 .
.
In the ideal case all parameters are perfectly known,
and the constraints would give curves in the 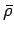 -
-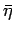 plane.
For example,
plane.
For example, 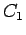 would give a circle of radius
would give a circle of radius 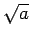 .
In other terms, due to this constraint all
points of the circumference would be appear to us likely,
unless
there is any other experimental piece of information
(or theoretical prejudice) to assign a different weight to
different points. In the ideal case
the p.d.f. describing our beliefs
in the
.
In other terms, due to this constraint all
points of the circumference would be appear to us likely,
unless
there is any other experimental piece of information
(or theoretical prejudice) to assign a different weight to
different points. In the ideal case
the p.d.f. describing our beliefs
in the 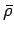 and
and 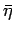 values would be
values would be
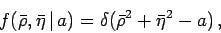 |
(1) |
with the Dirac delta meaning the limit
of a very narrow p.d.f. concentrated on the circumference.
Similar arguments hold for the parameters of the
other constraints. Let us call them generically 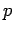 (the fact that
(the fact that 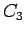 depends on two parameters is conceptually
irrelevant).
depends on two parameters is conceptually
irrelevant).
In the real case 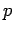 itself is not perfectly known.
There are values which are more likely, and values
which are less likely, classified
by the p.d.f.
itself is not perfectly known.
There are values which are more likely, and values
which are less likely, classified
by the p.d.f. 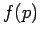 . This means that, e.g. for the parameter
. This means that, e.g. for the parameter 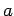 ,
we deal with an infinite number
of circles, each having its weight
,
we deal with an infinite number
of circles, each having its weight 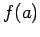 . It follows that the points
of the (
. It follows that the points
of the (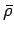 ,
, 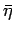 ) plane get different weights.
) plane get different weights.
The probability theory teaches us how to evaluate
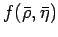 taking into account all possible values of
taking into account all possible values of 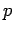 :
:
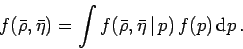 |
(2) |
Now the problem becomes how to evaluate 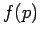 , knowing that
each
, knowing that
each 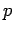 depends on many input quantities
depends on many input quantities 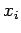 ,
denoted all together with
,
denoted all together with
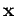 and described, in the most general case,
by a joint p.d.f.
and described, in the most general case,
by a joint p.d.f. 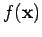 .
In most
cases of practical interest, including the one we are discussing,
each
.
In most
cases of practical interest, including the one we are discussing,
each 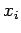 can be considered independent from the others,
and the joint distribution simplifies to
can be considered independent from the others,
and the joint distribution simplifies to
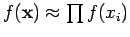 . Calling
. Calling 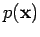 the function
which relates
the function
which relates 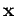 to
to 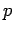 ,
, 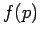 can be generally
obtained as
can be generally
obtained as
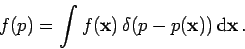 |
(3) |
This integral, as well as the previous integrals, is usually performed
by Monte Carlo techniques.
The calculations can be simplified in the following way.
- First, we rely on the central limit theorem, assuming
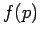 to be Gaussian
for all parameters (but with no constraint on the shape of
to be Gaussian
for all parameters (but with no constraint on the shape of
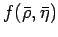 !).
!).
- Expected value, standard (deviation) uncertainty and correlation
are basically obtained by the usual propagation (see Ref. [5]
for a similar application).
- Non linear effects in the propagation have been taken into
account up to second order, using formulae of Ref. [6]
(see this paper for the practical modeling of uncertainties and
treatment of asymmetric cases).
- The correlation between
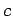 and
and 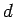 has been taken into account
building a bi-variate
has been taken into account
building a bi-variate 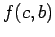 .
.
As input quantities, Table 1 of Ref. [1] is used, combining
properly (i.e. quadratically) the standard deviations.
For example, for
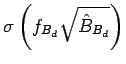 expressed in MeV we obtain
expressed in MeV we obtain
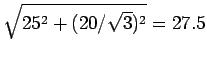 , where
, where
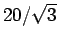 stands for the standard deviation
of a uniform distribution of half width 20 MeV.
Note that, contrary to what some authors critical
about Ref. [1] (and the related papers and presentations
to conferences) think, I have the impression that my colleagues
tend to make slightly conservative assessments
of uncertainties. This feeling that I had a priori
discussing with them is somewhat confirmed
a posteriori by the excellent overlap of the partial
inference by each constraint (as it will be shown in
Fig. 9) and self-consistency
between input parameters and values coming out of
the inference obtained without the their contribution
(see Ref. [1]).
stands for the standard deviation
of a uniform distribution of half width 20 MeV.
Note that, contrary to what some authors critical
about Ref. [1] (and the related papers and presentations
to conferences) think, I have the impression that my colleagues
tend to make slightly conservative assessments
of uncertainties. This feeling that I had a priori
discussing with them is somewhat confirmed
a posteriori by the excellent overlap of the partial
inference by each constraint (as it will be shown in
Fig. 9) and self-consistency
between input parameters and values coming out of
the inference obtained without the their contribution
(see Ref. [1]).
The following results are obtained in terms of expected values and
standard deviations (``
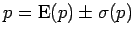 ''):
''):
Only the correlation between 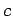 and
and 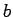 is relevant, and all
others can be neglected, being below the 10% level
(even that between
is relevant, and all
others can be neglected, being below the 10% level
(even that between 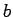 and
and 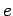 , related by
, related by 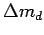 , is negligible,
being only +7%). The radii of the circles given by
, is negligible,
being only +7%). The radii of the circles given by 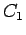 and
and 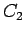 are
are 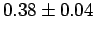 and
and 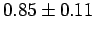 , respectively.
These radii have the meaning of the sides of the unitarity triangle opposite
to
, respectively.
These radii have the meaning of the sides of the unitarity triangle opposite
to 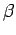 and
and 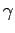 , respectively, provided
by
, respectively, provided
by 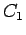 and
and 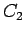 alone.
alone.



Next: Partial results from ,
Up: Inferring and of the
Previous: Introduction
Giulio D'Agostini
2004-01-20
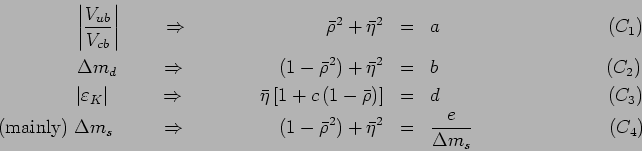
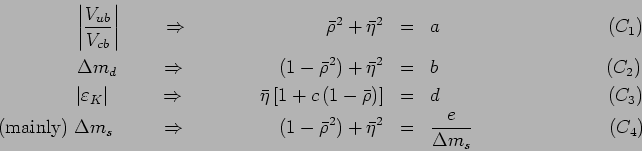
![]() -
-![]() plane.
For example,
plane.
For example, ![]() would give a circle of radius
would give a circle of radius ![]() .
In other terms, due to this constraint all
points of the circumference would be appear to us likely,
unless
there is any other experimental piece of information
(or theoretical prejudice) to assign a different weight to
different points. In the ideal case
the p.d.f. describing our beliefs
in the
.
In other terms, due to this constraint all
points of the circumference would be appear to us likely,
unless
there is any other experimental piece of information
(or theoretical prejudice) to assign a different weight to
different points. In the ideal case
the p.d.f. describing our beliefs
in the ![]() and
and ![]() values would be
values would be
![]() itself is not perfectly known.
There are values which are more likely, and values
which are less likely, classified
by the p.d.f.
itself is not perfectly known.
There are values which are more likely, and values
which are less likely, classified
by the p.d.f. ![]() . This means that, e.g. for the parameter
. This means that, e.g. for the parameter ![]() ,
we deal with an infinite number
of circles, each having its weight
,
we deal with an infinite number
of circles, each having its weight ![]() . It follows that the points
of the (
. It follows that the points
of the (![]() ,
, ![]() ) plane get different weights.
) plane get different weights.
![]() taking into account all possible values of
taking into account all possible values of ![]() :
:
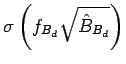 expressed in MeV we obtain
expressed in MeV we obtain
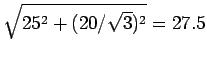 , where
, where
![]() stands for the standard deviation
of a uniform distribution of half width 20 MeV.
Note that, contrary to what some authors critical
about Ref. [1] (and the related papers and presentations
to conferences) think, I have the impression that my colleagues
tend to make slightly conservative assessments
of uncertainties. This feeling that I had a priori
discussing with them is somewhat confirmed
a posteriori by the excellent overlap of the partial
inference by each constraint (as it will be shown in
Fig. 9) and self-consistency
between input parameters and values coming out of
the inference obtained without the their contribution
(see Ref. [1]).
stands for the standard deviation
of a uniform distribution of half width 20 MeV.
Note that, contrary to what some authors critical
about Ref. [1] (and the related papers and presentations
to conferences) think, I have the impression that my colleagues
tend to make slightly conservative assessments
of uncertainties. This feeling that I had a priori
discussing with them is somewhat confirmed
a posteriori by the excellent overlap of the partial
inference by each constraint (as it will be shown in
Fig. 9) and self-consistency
between input parameters and values coming out of
the inference obtained without the their contribution
(see Ref. [1]).
![]() ''):
''):