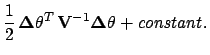Next: Uncertainties from systematic effects
Up: Inferring numerical values of
Previous: From Bayesian inference to
Gaussian approximation of the posterior distribution
The substance of the results seen in the previous section
holds also in the case in which the prior is not flat and, hence,
cannot be absorbed in the normalization constant of the posterior.
In fact, in many practical cases the posterior exhibits an approximately
(multi-variate) Gaussian shape, even if the prior was not trivial.
Having at hand an un-normalized posterior 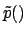 , i.e.
, i.e.
we can take its minus-log function
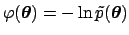 .
If
.
If
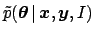 has
approximately a Gaussian shape, it follows that
has
approximately a Gaussian shape, it follows that
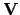 can be evaluated as
can be evaluated as
where
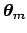 was obtained from the
minimum of
was obtained from the
minimum of
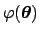 .
.



Next: Uncertainties from systematic effects
Up: Inferring numerical values of
Previous: From Bayesian inference to
Giulio D'Agostini
2003-05-13