


Next: Joint inference and marginalization
Up: Uncertainties from systematic effects
Previous: Uncertainties from systematic effects
Reweighting of conditional inferences
The values of the influence variables and their uncertainties
contribute to our background knowledge 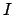 about the experimental
measurements. Using
about the experimental
measurements. Using 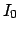 to represent our very general background
knowledge, the posterior pdf
will then be
to represent our very general background
knowledge, the posterior pdf
will then be
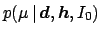 , where the dependence on
all possible values of
, where the dependence on
all possible values of
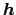 has been made explicit. The
inference that takes into account the uncertain vector
has been made explicit. The
inference that takes into account the uncertain vector
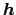 is
obtained using the rules of probability (see Tab. 1)
by integrating the joint probability over the uninteresting
influence variables:
is
obtained using the rules of probability (see Tab. 1)
by integrating the joint probability over the uninteresting
influence variables:
As a simple, but important case, let us consider a single
influence variable given by an additive instrumental offset
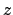 , which is expected to
be zero because the instrument has been calibrated as well as feasible and
the remaining uncertainty is
, which is expected to
be zero because the instrument has been calibrated as well as feasible and
the remaining uncertainty is 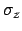 . Modelling our
uncertainty in
. Modelling our
uncertainty in 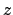 as a Gaussian distribution with a standard
deviation
as a Gaussian distribution with a standard
deviation 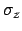 , the posterior for
, the posterior for 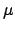 is
is
The result is that the net variance is the sum of
the variance in the measurement and the variance in the influence variable.



Next: Joint inference and marginalization
Up: Uncertainties from systematic effects
Previous: Uncertainties from systematic effects
Giulio D'Agostini
2003-05-13
![]() about the experimental
measurements. Using
about the experimental
measurements. Using ![]() to represent our very general background
knowledge, the posterior pdf
will then be
to represent our very general background
knowledge, the posterior pdf
will then be
![]() , where the dependence on
all possible values of
, where the dependence on
all possible values of
![]() has been made explicit. The
inference that takes into account the uncertain vector
has been made explicit. The
inference that takes into account the uncertain vector
![]() is
obtained using the rules of probability (see Tab. 1)
by integrating the joint probability over the uninteresting
influence variables:
is
obtained using the rules of probability (see Tab. 1)
by integrating the joint probability over the uninteresting
influence variables: