Conclusions

The gain in popularity Bayesian methods have enjoyed in recent years is due to various conceptual and practical advantages they have over other approaches, among which are:

• the recovery of the intuitive idea of probability as a valid concept for treating scientific problems;
• the simplicity and naturalness of the basic tool;
• the capability of combining prior knowledge and experimental information;
• the property permitting automatic updating as soon as new information becomes available;
• the transparency of the methods, which allow the different assumptions upon which an inference may depend to be checked and changed;
• the high degree of awareness the methods give to the user.

In this article we have seen how to build a theory of uncertainty in measurement as a straightforward application of the basic Bayesian ideas, without unnecessary principles or ad hoc prescriptions. In particular, the uncertainty due to systematic errors can be treated in a consistent and powerful way.

Providing an exact solution for inferential problems can easily lead to computational difficulties. We have seen several ways to overcome such difficulties, either by using suitable approximations, or by using modern computational methods. In particular, it has been shown that the approximate solution often coincides with a `conventional' method, but only under well defined conditions. Thus, for example, minimum 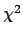$\chi^2$ formulae can be used, with a Bayesian spirit and with a natural interpretation of the results, in all those routine cases in which the analyst considers as reasonable the conditions of their validity.

A variety of examples of applications have been shown, or mentioned, in this paper. Nevertheless, the aim of the author was not to provide a complete review of Bayesian methods and applications, but rather to introduce those Bayesian ideas that could be of help in understanding more specialized literature. Compendia of the Bayesian theory are given in (Bernardo and Smith 1994, O'Hagan A 1994 and Robert 2001). Classic, influential books are (Jeffreys 1961, de Finetti 1974, Jaynes 1998). Among the many books introducing Bayesian methods, (Sivia 1996) is particularly suitable for physicists. Other recommended texts which treat general aspects of data analysis are (Box and Tiao 1973, Bretthorst 1988, Lee 1989, Gelman et al 1995, Cowell et al 1999, Denison et al 2002, Press 2002). More specific applications can be found in the proceedings of the conference series and several web sites. Some useful starting points for web navigation are given:

ISBA book list	http://www.bayesian.org/books/books.html
UAI proceedings	http://www2.sis.pitt.edu/ dsl/UAI/uai.html
BIPS	http://astrosun.tn.cornell.edu/staff/loredo/bayes/
BLIP	http://www.ar-tiste.com/blip.html
IPP Bayesian analysis group	http://www.ipp.mpg.de/OP/Datenanalyse/
Valencia meetings	http://www.uv.es/~bernardo/valenciam.html
Maximum Entropy resources	http://omega.albany.edu:8008/maxent.html
MCMC preprint service	http://www.statslab.cam.ac.uk/~mcmc/

I am indebted to Volker Dose and Ken Hanson for extensive discussions concerning the contents of this paper, as well as for substantial editorial help. The manuscript has also benefited from comments by Tom Loredo.

References

Astone P et al 2002 Search for correlation between GRB's detected by BeppoSAX and gravitational wave detectors EXPLORER and NAUTILUS Phys. Rev. 66 102002.

Astone P and D'Agostini G 1999 Inferring the intensity of Poisson processes at limit of detector sensitivity (with a case study on gravitational wave burst search) CERN-EP/99-126

Astone P, D'Agostini G and D'Antonio 2003 Bayesian model comparison applied to the Explorer-Nautilus 2001 coincidence data, arXiv:gr-qc/0304096

Babu G J and Feigelson E D 1992 eds Statistical Challenges in Modern Astronomy I (New York: Springer)

Babu G J and Feigelson E D 1997 eds Statistical Challenges in Modern Astronomy II (New York: Springer)

Berger J O and Jefferys W H 1992 Sharpening Ockham's razor on a Bayesian strop Am. Scientist 89 64-72 and J. Ital. Stat. Soc. 1 17

Bernardo J M 1999 ed Bayesian Methods in the Sciences, special issue of Rev. Acad. Cien. Madrid, 93(3)

Bernardo J M, J O Berger, A P Dawid and A F M Smith 1999 eds Bayesian Statistics 6 (Oxford: Oxford University)

Bernardo J M and Smith F M 1994 Bayesian Theory (Chichester: John Wiley & Sons)

Bernardo J M 1997 Non-informative priors do not exist J. Stat. Planning and Infer. 65 159

Bontekoe T R, Koper E and Kester D J M 1994 Pyramid maximum entropy images of IRAS survey data Astron. Astrophys. 284 1037

Bouman C A and Sauer K 1993 A generalized Gaussian image model for edge-preserving MAP estimation IEEE Trans. on Image Processing 2 296

Box G E P and Tiao G C 1973 Bayesian inference in statistical analysis (Chichester: J. Wiley & Sons)

Bretthorst G L 1988 Bayesian spectrum analysis and parameter estimation (Berlin: Springer)

BUGS 1996 http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml

Buck B and Macauly V A eds 1991 Maximum Entropy in action, (Oxford: Oxford University Press)

Ciuchini M et al 2001 2000 CKM-Triangle Analysis: A critical review with updated experimental inputs and theoretical parameters J. High Energy Phys. 0107 013

Coletti G and Scozzafava R 2002 Probabilistic logic in a coherent setting'', (Dordrecht: Kluwer Academic)

Cousins R D 1995 Why isn't every physicist a Bayesian? Am. J. Phys. 63 398

Cowell R G, Dawid A P, Lauritzen S L and Spiegelhalter D J 1999 Probabilistic Networks and Expert Systems, (New York: Springer)

Cox R T 1946 Probability, Frequency and Reasonable Expectation Am. J. Phys. 14 1

Cozman F B 2001 JavaBayes version 0.346 - Bayesian networks in Java http://www-2. cs.cmu.edu/~javabayes/Home/

Cunningham G S, Hanson K M and Battle X L 1998 Three-dimensional reconstructions from low-count SPECT data using deformable models Opt. Expr. 2 227

D'Agostini G 1999a Bayesian Reasoning versus Conventional Statistics in High Energy Physics Maximum Entropy and Bayesian Methods ed von der Linden W et al (Dordrecht: Kluwer Academic)

D'Agostini G 1999b Sceptical combination of experimental results: General considerations and application to epsilon-prime/epsilon CERN-EP/99-139

D'Agostini G 1999c Bayesian reasoning in high-energy physics: principles and applications CERN Report 99-03 (an extended version of this report is going to be published as Bayesian reasoning in data analysis - A critical introduction by World Scientific Publishing)

D'Agostini G 1999d Teaching statistics in the physics curriculum: Unifying and clarifying role of subjective probability Am. J. Phys. 67 1260

D'Agostini G 1999e Overcoming prior Anxiety, Bayesian Methods in the Sciences ed J. M. Bernardo; special issue of Rev. Acad. Cien. Madrid 93(3), 311

D'Agostini G 2000 Confidence limits: what is the problem? Is there the solution? CERN Report 2000-005 ed James F and Lyons L (Geneva: CERN) 3

D'Agostini G 2002 Minimum bias legacy of search results 2002 Nucl Phys Proc Suppl 109 148

D'Agostini G and Degrassi G 1999 Constraints on the Higgs Boson Mass from Direct Searches and Precision Measurements Eur. Phys. J. C10 663

D'Agostini G and Raso M Uncertainties due to imperfect knowledge of systematic effects: general considerations and approximate formulae CERN-EP/2000-026

de Finetti B 1974 Theory of Probability (Chichester: J. Wiley & Sons)

Denison D G T, Holmes C C, Mallick B K and Smith A F M 2002 Bayesian methods for nonlinear classification and regression (Cichester: J. Wiley & Sons)

DIN (Deutsches Institut für Normung) 1996 Grundlagen der Messtechnik - Teil 3: Auswertung von Messungen einer einzelnen Messgröße, Messunsicherheit DIN 1319-3 (Berlin: Beuth Verlag)

DIN (Deutsches Institut für Normung) 1999 Grundlagen der Messtechnik - Teil 4: Auswertung von Messungen, Messunsicherheit DIN 1319-4 (Berlin: Beuth Verlag)

Dose V 2002 Bayes in five days, CIPS, MPI für Plasmaphysik, Garching, Germany, Reprint 83, May 2002

Dose V and von der Linden W 1999 Outlier tolerant parameter estimation Maximum Entropy and Bayesian Methods ed von der Linden W et al (Dordrecht: Kluwer Academic) 47

Efron B 1986a Why isn't everyone a Bayesian? Am. Stat. 40 1

Efron B 1986b reply to Zellner 1986 Am. Stat. 40 331

Fischer R, Mayer M, von der Linden W and Dose V 1997 Enhancement of the energy resolution in ion-beam experiments with the maximum-entropy method Phys. Rev. E 55 6667

Fischer R, Mayer M, von der Linden W and Dose V 1998 Energy resolution enhancement in ion beam experiments with Bayesian probability theory Nucl. Instr. Meth. 136-138 1140

Fischer R, Hanson K M, Dose V and von der Linden W 2000 Background estimation in experimental spectra Phys. Rev. E61 1152

Fröhner F H 2000 Evaluation and Analysis of Nuclear Resonance Data JEFF Report 18 (Paris: OECD Publications)

Gelman A, Carlin J B, Stern H S and Rubin D B 1995 Bayesian Data Analysis (London: Chapman and Hall)

Glimm J and Sharp D H 1999 Prediction and the quantification of uncertainty Physica D 133 152

Gregory P C and Loredo T J 1992 A new method for the detection of a periodic signal of unknown shape and period Astr. J. 398 146

Gregory P C and Loredo T J 1996 Bayesian periodic signal detection II - Bayesian periodic signal detection: analysis of ROSAT observations of PSR 0540-693 Astr. J. 473 1059

Gregory P C 1999 Bayesian periodic signal detection I - analysis of 20 years of radio flux measurements of the x-ray binary LS I +61$^\circ$303 Astr. J. 520 361

Gubernatis J E, Jarrell M, Silver R N and Sivia D S 1991 Quantum Monte-Carlo simulations and maximum-entropy: dynamics from imaginary-time data Phys. Rev. B 44 6011

Hanson K M 1993 Introduction to Bayesian image analysis Medical Imaging: Image Processing Loew M H ed Proc. SPIE 1898 716

Hanson K M 2000 Tutorial on Markov Chain Monte Carlo, http://public.lanl.gov/ kmh/talks/maxent00b.pdf

Hasting W K 1970 Monte Carlo sampling methods using Markov chains and their applications Biometrica 57 97

Higdon D M and Yamamoto S Y 2001 Estimation of the head sensitivity function in scanning magnetoresistance microscopy J. Amer. Stat. Assoc. 96 785

Hobson M P, Bridle S L and Lahav 2002 Combining cosmological datasets: hyperparameters and Bayesian evidence arXiv:astro-ph/0203259

Howson C and Urbach P 1993 Scientific reasoning -- the Bayesian approach (Chicago and La Salle: Open Court)

ISO (International Organization for Standardization) 1993 Guide to the Expression of Uncertainty in Measurement (Geneva: ISO)

Jaynes E T 1957a Information theory and statistical mechanics Phys. Rev. 106 620

Jaynes E T 1957b Information theory and statistical mechanics II Phys. Rev. 108 171

Jaynes E T 1968 Prior probabilities IEEE Trans. Syst. Cybern. SSC-4 227, reprinted in (Jaynes 1983)

Jaynes E T 1973 The well-posed problem Found. Phys. 3 477, reprinted in (Jaynes 1983)

Jaynes E T 1983 Papers on Probability, Statistics and Statistical Physics ed Harper W L and Hooker C A (Dordrecht: Reidel)

Jaynes E T 1998 http://omega.albany.edu:8008/JaynesBook.html

Jeffreys H 1961 Theory of Probability (Oxford: Oxford University)

John M V and Narlikar J V 2002 Comparison of cosmological models using Bayesian theory Phys. Rev. D65 43506

Kadane J B and Schum D A 1996 A Probabilistic Analysis of the Sacco and Vanzetti Evidence (Chichester: Wiley and Sons)

Kalman R E 1960 A new approach to linear filtering and prediction problems Trans. ASME Journal of Casic Engineering 82 35

Kass R E, Carlin B P, Gelman A and Neal R M 1998 Markov Chain Monte Carlo in practice: A roundtable discussion Am. Stat. 52 93

Lad F 1996 Operational Subjective Statistical Methods - a Mathematical, Philosophical, and Historical Introduction (Chichester:J. Wiley & Sons)

Lee P M 1989 Bayesian statistics - an introduction (Chichester:J. Wiley & Sons)

Lewis A and Bridle S 2002 Cosmological parameters from CMB and other data: a Monte-Carlo approach Phys.Rev. D66 103511

von der Linden W 1995 Maximum-entropy data analysis Appl. Phys. A60 155

von der Linden W, Dose V and Fischer R 1996b Spline-based adaptive resolution image reconstruction Proceedings of the 1996 Maximum Entropy Conference ed Sears M et al (Port Elizabeth: N.M.B. Printers) 154

Lindley D V 1986 Discussion to Efron 1986a Am. Stat. 40 6

Loredo T J 1990 Maximum Entropy and Bayesian Methods ed Fougére P F (Dordrecht: Kluwer Academic) 81

Loredo T J and Lamb D Q 2002 Bayesian analysis of neutrinos observed from supernova SN 1987A Phys. Rev. D65 063002

Malakoff D 1999 Bayes Offers a 'New' Way to Make Sense of Numbers Science 286 1460

Maybaeck P S 1979 Stochastic models, estimation and control, Vol. 1 (New York: Academic Press).

Metropolis H, Rosenbluth A W, Rosenbluth M N, Teller A H and Teller E 1953 Equations of state calculations by fast computing machines Journal of Chemical Physics 21 1087

von Mises R 1957 Probability, Statistics, and Truth (St Leonards: Allen and Unwin); reprinted in 1987 by Dover

Neal R M 1993 Probabilistic inference using Markov chain Monte Carlo methods (Toronto: Technical Report CRG-TR-93-1)

O'Hagan A 1994 Kendall's Advanced Theory of Statistics: Vol. 2B - Bayesian Inference (New York: Halsted)

Pearl J 1988 Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference (San Mateo: Morgan Kaufmann)

Press W H 1997 Understanding data better with Bayesian and global statistical methods Unsolved problems in astrophysics49-60 ed Bahcall J N and Ostriker J P (Princeton: Princeton University) 49

Press S J 2002 Subjective and Objective Bayesian Statistics: Principles, Models, and Applications 2nd Edition (Chichester: John Wiley & Sons)

Robert C P 2001 The Bayesian Choice (New York: Springer)

Saquib S S, Hanson K M, and Cunningham G S 1997 Model-based image reconstruction from time-resolved diffusion data Proc. SPIE 3034 369

Schrödinger E 1947a The Foundation of the Theory of Probability - I Proc. R. Irish Acad. 51A 51; reprinted in Collected papers Vol. 1 (Vienna 1984: Austrian Academy of Science) 463

Schrödinger E 1947b The Foundation of the Theory of Probability - II Proc. R. Irish Acad. 51A 141; reprinted in Collected papers Vol. 1 (Vienna 1984: Austrian Academy of Science) 479

Sivia D S 1997 Data Analysis - a Bayesian Tutorial (Oxford: Clarendon)

Skilling J 1992 Quantified maximum entropy Int. Spectr. Lab. 2 4

Smith A F M 1991 Bayesian numerical analysis Phyl. Trans. R. Soc. London 337 369

Taylor B N and Kuyatt C E 1994 Guidelines for Evaluating and Expressing Uncertainty of NIST Measurement Results (Gaithersburg: NIST Technical Note 1297); available on line at http://physics.nist.gov/

Tribus M 1969 Rational Descriptions, Decisions, and Designs (Elmsford: Pergamon)

Welch G and Bishop G 2002 An introduction to Kalman filter (http://www.cs.unc. edu/~welch/kalman/)

Zech G 2002 Frequentist and Bayesian confidence limits Eur. Phys. J. direct C12 1

Zellner A 1986 Bayesian solution to a problem posed by Efron Am. Stat. 40 330