Foreword

We have seen the use of jupyter notebooks.
As a matter of fact these slides are a notebook converted to (HTML) slides via the jupyter-nbconvert utility.
Get the code from gitlab here: https://gitlab.com/carlomt/pycourse with, in an new terminal:

git clone https://gitlab.com/carlomt/pycourse
cd pycourse
conda env create -f environment.yml
conda activate pycourse
. post-install.sh #Configure some extra stuff

The pre-installed environment course is enough to read/edit these slides.
Read the README.md file for additional instructions.

Python Introduction Course: Data Science tools

With emphasis on data-science problems

This course is available on gitlab
Contact us: andrea.dotti@gmail.com, mancinit@infn.it

Scientific python stack

Get full documentation here.
Get a tutorial here

The SciPy library contains several packages to perform specialized scientific calculations:

Numpy

It is the foundation of python scientific stack.
The basic building block is the numpy.array data structure. It can be used as a python list of numbers, but it is a specialized efficient way of manipulating numbers in python.

In [4]:
import numpy as np
a = np.array([1, 2, 3, 4], dtype=float)
a
Out[4]:
array([1., 2., 3., 4.])
In [7]:
a = range(1000)
%timeit [ i**2 for i in a]

222 µs ± 3.93 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
In [8]:
b = np.arange(1000)
%timeit b**2

1.61 µs ± 10.6 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
In [10]:
c = np.array([[1,2],[3,4]])
c
Out[10]:
array([[1, 2],
       [3, 4]])
In [11]:
c.ndim
Out[11]:
2
In [12]:
c.shape
Out[12]:
(2, 2)
In [13]:
c = np.arange(27)
c.reshape((3,3,3))
Out[13]:
array([[[ 0,  1,  2],
        [ 3,  4,  5],
        [ 6,  7,  8]],

       [[ 9, 10, 11],
        [12, 13, 14],
        [15, 16, 17]],

       [[18, 19, 20],
        [21, 22, 23],
        [24, 25, 26]]])
In [14]:
np.zeros((2,2))
Out[14]:
array([[0., 0.],
       [0., 0.]])
In [15]:
np.ones((2,1))
Out[15]:
array([[1.],
       [1.]])
In [18]:
a = np.arange(27).reshape((3,3,3))
np.ones_like(a)
Out[18]:
array([[[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]],

       [[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]],

       [[1, 1, 1],
        [1, 1, 1],
        [1, 1, 1]]])
In [19]:
np.eye(3)
Out[19]:
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
In [23]:
a = np.arange(10)
a
Out[23]:
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [24]:
a[0]
Out[24]:
0
In [25]:
a[-1]
Out[25]:
9
In [26]:
a[0:3]
Out[26]:
array([0, 1, 2])
In [27]:
a[::2]
Out[27]:
array([0, 2, 4, 6, 8])
In [35]:
a = a.reshape(5,2)
a
Out[35]:
array([[0, 1],
       [2, 3],
       [4, 5],
       [6, 7],
       [8, 9]])
In [33]:
a[3,1]
Out[33]:
7
In [34]:
a[2,:]
Out[34]:
array([4, 5])

Important: Views or copy

A slice or reshape is a view, simply a re-organization of the same data in memory, thus changing one element changes the same element in all views

In [41]:
a = np.arange(9)
In [42]:
b = a.reshape((3,3))
In [43]:
np.may_share_memory(a,b)
Out[43]:
True
In [44]:
a[3] = -1
In [45]:
b
Out[45]:
array([[ 0,  1,  2],
       [-1,  4,  5],
       [ 6,  7,  8]])
In [46]:
b = a.copy()
np.may_share_memory(a,b)
Out[46]:
False

Boolean masks for extracting values

A typical operation done in your daily physics data analysis is to extract from an array the values that match a condition. Consider an array of the energies of particles, and assume you want to use only the energies above a given threshold. Boolean masking comes at a rescue

In [52]:
ene = np.random.exponential(size=10, scale=10.) # 1/scale e^(-ene/scale)
ene
Out[52]:
array([ 4.85456007,  0.51860863,  3.69385318,  5.40459025,  3.83217684,
        5.31482774,  0.20313695,  7.66005641,  2.52100998, 12.84343854])
In [54]:
mask = ene > 2
mask
Out[54]:
array([ True, False,  True,  True,  True,  True, False,  True,  True,
        True])
In [55]:
ene[mask]
Out[55]:
array([ 4.85456007,  3.69385318,  5.40459025,  3.83217684,  5.31482774,
        7.66005641,  2.52100998, 12.84343854])
In [56]:
ene[ene<2]
Out[56]:
array([0.51860863, 0.20313695])
In [57]:
ene[ene<2] = 0
ene
Out[57]:
array([ 4.85456007,  0.        ,  3.69385318,  5.40459025,  3.83217684,
        5.31482774,  0.        ,  7.66005641,  2.52100998, 12.84343854])

Values with list of indexes

Similarly to boolean masks it is possible to access and modify values directly to an array using a list of indexes

In [60]:
status = np.random.randint(low=0,high=10,size=10)
status
Out[60]:
array([2, 7, 7, 7, 8, 6, 0, 7, 4, 4])
In [61]:
status[[0, 3, 5]]
Out[61]:
array([2, 7, 6])
In [63]:
status[[0, 3, 5]] = -1
status
Out[63]:
array([-1,  7,  7, -1,  8, -1,  0,  7,  4,  4])

Simple Operations

In [64]:
a = np.arange(4)
a
Out[64]:
array([0, 1, 2, 3])
In [65]:
a+1
Out[65]:
array([1, 2, 3, 4])
In [67]:
10**a
Out[67]:
array([   1,   10,  100, 1000])
In [68]:
np.sin(a)
Out[68]:
array([0.        , 0.84147098, 0.90929743, 0.14112001])

Reductions

In [78]:
a = np.random.randint(low=0,high=10,size=4)
a
Out[78]:
array([1, 8, 0, 9])
In [90]:
np.sum(a)
Out[90]:
18
In [91]:
np.max(a), np.min(a)
Out[91]:
(9, 0)
In [92]:
np.argmax(a), np.argmin(a)
Out[92]:
(3, 2)
In [93]:
np.mean(a), np.median(a), np.std(a)
Out[93]:
(4.5, 4.5, 4.031128874149275)
In [94]:
a = a.reshape(2,2)
a
Out[94]:
array([[1, 8],
       [0, 9]])
In [95]:
np.sum(a,axis=0)
Out[95]:
array([ 1, 17])
In [84]:
m1 = a>0
m1
Out[84]:
array([[ True,  True],
       [False,  True]])
In [96]:
np.all(m1)
Out[96]:
False
In [97]:
np.any(m1)
Out[97]:
True

Matplotlib

Matplotlib is probably the most used Python package for 2D-graphics. It provides both a quick way to visualize data from Python and publication-quality figures in many formats.
Other visualization packages exists, often these are built on top of matplotlib. The package is well integrated into IPython and Jupyter.

In [114]:
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
X = np.linspace(-np.pi, np.pi, 256, endpoint=True)
C, S = np.cos(X), np.sin(X)
plt.plot(X,C)
plt.plot(X,S)
Out[114]:
[<matplotlib.lines.Line2D at 0x7f6c7a21c4e0>]

Customization

In [125]:
plt.figure(figsize=(4, 3), dpi=80)
plt.plot(X, C, color="blue", linewidth=1.0, linestyle="-", label="cos")
plt.plot(X, S, color="green", linewidth=1.0, linestyle="-", label="sin")
plt.xlim(-4.0, 4.0)
plt.xticks(np.linspace(-4, 4, 9, endpoint=True))
plt.savefig("example.png", dpi=72)
plt.grid()
plt.xlabel("x")
plt.ylabel("y")
plt.title("Example")
plt.legend(loc="best")
Out[125]:
<matplotlib.legend.Legend at 0x7f6c79c0bc18>

Multiple plots

In [124]:
plt.figure(figsize=(6, 4))
plt.subplot(2, 2, 1)
plt.plot(X, C, color="blue", linewidth=1.0, linestyle="-", label="cos")
plt.subplot(2, 2, 2)
plt.plot(X, S, color="green", linewidth=1.0, linestyle="-", label="sin")
plt.subplot(2, 2, 3)
plt.plot(X, C, color="red", linewidth=1.0, linestyle="-", label="cos")
plt.subplot(2, 2, 4)
plt.plot(X, S, color="black", linewidth=1.0, linestyle="-", label="sin")
plt.show()

Examples

In [131]:
plt.rcdefaults()
fig, ax = plt.subplots(figsize=(4,3))
# Example data
people = ('Tom', 'Dick', 'Harry', 'Slim', 'Jim')
y_pos = np.arange(len(people))
performance = 3 + 10 * np.random.rand(len(people))
error = np.random.rand(len(people))
ax.barh(y_pos, performance, xerr=error, align='center',
        color='green', ecolor='black')
ax.set_yticks(y_pos)
ax.set_yticklabels(people)
ax.invert_yaxis()  # labels read top-to-bottom
ax.set_xlabel('Performance')
ax.set_title('How fast do you want to go today?')

plt.show()
In [132]:
x = np.linspace(0, 1, 500)
y = np.sin(4 * np.pi * x) * np.exp(-5 * x)
fig, ax = plt.subplots()
ax.fill(x, y, zorder=10)
ax.grid(True, zorder=5)
plt.show()
In [136]:
fig, ax = plt.subplots()
for color in ['red', 'green', 'blue']:
    n = 750
    x, y = np.random.rand(2, n)
    scale = 200.0 * np.random.rand(n)
    ax.scatter(x, y, c=color, s=scale, label=color,
               alpha=0.3, edgecolors='none')

ax.legend()
ax.grid(True)

plt.show()
In [161]:
mu = 200
sigma = 25
x = np.random.normal(mu, sigma, size=100)
fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(6, 3))
ax0.hist(x, 20, density=1, histtype='stepfilled', facecolor='g', alpha=0.75)
ax0.set_title('stepfilled')
# Create a histogram by providing the bin edges (unequally spaced).
bins = [100, 150, 180, 195, 205, 220, 250, 300]
ax1.hist(x, bins, density=1, histtype='bar', rwidth=0.8)
ax1.set_title('unequal bins')
plt.title(r'Histogram of IQ: $\mu=100$, $\sigma=15$');
In [170]:
from matplotlib import colors, ticker, cm
from scipy.stats import multivariate_normal

N = 100
x = np.linspace(-3.0, 3.0, N)
y = np.linspace(-2.0, 2.0, N)

X, Y = np.meshgrid(x, y)
pos = np.empty(X.shape+(2,))
pos[:,:,0] = X; pos[:,:,1] = Y
# A low hump with a spike coming out of the top right.
# Needs to have z/colour axis on a log scale so we see both hump and spike.
# linear scale only shows the spike.
z = (multivariate_normal([0.1, 0.2], [[1.0, 0.],[0, 1.0]]).pdf(pos)
     + 0.1 * (multivariate_normal([1.0, 1.0],[[0.01, 0.],[0., 0.01]])).pdf(pos))
# Automatic selection of levels works; setting the
# log locator tells contourf to use a log scale:
fig, ax = plt.subplots(figsize=(4,3))
cs = ax.contourf(X, Y, z, locator=ticker.LogLocator(), cmap=cm.PuBu_r)
cbar = fig.colorbar(cs)

Pandas

Pandas is a high-performance, high-level library that provides tools for data analysis.
It relies on the concept of DataFrame: a structured collection of data organized in records. This is the same concept of ROOT's NTuple that you are familiar with.
I think the name comes from R.

In [2]:
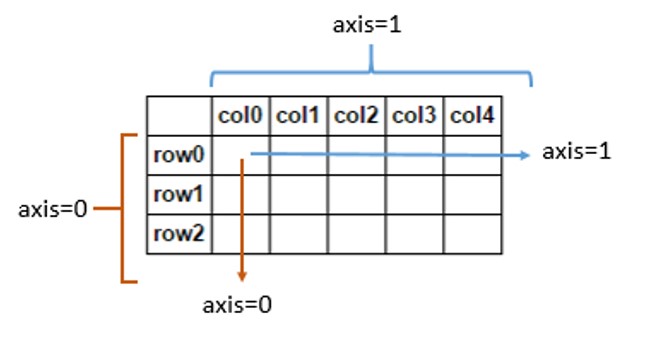
import numpy as np
import pandas as pd

s = pd.Series( [1., 2., 3., np.nan, 5. ], index=["a","b","c","d","e"])
s
Out[2]:
a    1.0
b    2.0
c    3.0
d    NaN
e    5.0
dtype: float64
In [11]:
df = pd.DataFrame( 
    {
        'Col1': [1.,2.,3.,4.],
        'Col2': ["a","b","c","d"],
        'Col3': [True, False, True, True]
    }
)
df
Out[11]:
Col1 Col2 Col3
0 1.0 a True
1 2.0 b False
2 3.0 c True
3 4.0 d True

Reading/Saving dataframes

Pandas support reading writing to several data formats, via specialized routines, many other formats, because dataframe (with other names) are a common concept:

Format Type Data Description Reader Writer
text CSV read_csv to_csv
text JSON read_json to_json
text HTML read_html to_html
text Local clipboard read_clipboard to_clipboard
binary MS Excel read_excel to_excel
binary HDF5 Format read_hdf to_hdf
binary Feather Format read_feather to_feather
binary Parquet Format read_parquet to_parquet
binary Msgpack read_msgpack to_msgpack
binary Stata read_stata to_stata
binary SAS read_sas
binary Pickle Format read_pickle to_pickle
SQL SQL read_sql to_sql
SQL Google Big Query read_gbq to_gbq

As you can see the physicists ROOT format is not natively supported. However some external software to read TTrees are available. For example root_numpy, root_pandas, or uproot. ROOT usually comes with pre-installed pyROOT library (the one on the provided VM works only for python2), that offers basic functionalities.

In [12]:
df.dtypes
Out[12]:
Col1    float64
Col2     object
Col3       bool
dtype: object
In [13]:
df.columns
Out[13]:
Index(['Col1', 'Col2', 'Col3'], dtype='object')
In [14]:
df.index
Out[14]:
RangeIndex(start=0, stop=4, step=1)

View data

In [25]:
df = pd.DataFrame( {'A':np.random.randint(0,10,100), 'B': [2**x for x in np.arange(100)], 'C':"a"})
df.head()
Out[25]:
A B C
0 4 1 a
1 2 2 a
2 0 4 a
3 9 8 a
4 3 16 a
In [26]:
df.tail(2)
Out[26]:
A B C
98 5 0 a
99 9 0 a
In [27]:
df.describe()
Out[27]:
A B
count 100.000000 1.000000e+02
mean 4.420000 -2.560000e+00
std 2.985419 1.070389e+18
min 0.000000 -9.223372e+18
25% 2.000000 0.000000e+00
50% 5.000000 6.144000e+03
75% 7.000000 1.717987e+11
max 9.000000 4.611686e+18

Select data

In [86]:
dates = pd.date_range('20190527',periods=7)
df = pd.DataFrame( np.random.rand(7,4), index=dates, columns=['A','B','C','D'])
df
Out[86]:
A B C D
2019-05-27 0.944420 0.075201 0.167932 0.017186
2019-05-28 0.245307 0.577804 0.132167 0.372844
2019-05-29 0.459021 0.087459 0.647909 0.963480
2019-05-30 0.244232 0.261606 0.109693 0.494399
2019-05-31 0.575183 0.584652 0.113913 0.117457
2019-06-01 0.190005 0.692712 0.404453 0.995082
2019-06-02 0.931300 0.489561 0.193387 0.327648
In [43]:
df['A'] # or df.A
Out[43]:
2019-05-27    0.632271
2019-05-28    0.691208
2019-05-29    0.603331
2019-05-30    0.043723
2019-05-31    0.552101
2019-06-01    0.330455
2019-06-02    0.841736
Freq: D, Name: A, dtype: float64
In [44]:
df[0:2]
Out[44]:
A B C D
2019-05-27 0.632271 0.218192 0.139538 0.082094
2019-05-28 0.691208 0.700231 0.730246 0.328330
In [45]:
df['20190529':'20190531']
Out[45]:
A B C D
2019-05-29 0.603331 0.165942 0.199283 0.119786
2019-05-30 0.043723 0.162669 0.291625 0.120803
2019-05-31 0.552101 0.102359 0.702799 0.455912
In [46]:
dates
Out[46]:
DatetimeIndex(['2019-05-27', '2019-05-28', '2019-05-29', '2019-05-30',
               '2019-05-31', '2019-06-01', '2019-06-02'],
              dtype='datetime64[ns]', freq='D')
In [47]:
df.loc[dates[2]]
Out[47]:
A    0.603331
B    0.165942
C    0.199283
D    0.119786
Name: 2019-05-29 00:00:00, dtype: float64
In [48]:
df.loc[dates[2],['B','C']]
Out[48]:
B    0.165942
C    0.199283
Name: 2019-05-29 00:00:00, dtype: float64
In [53]:
df.iloc[2,2:4]
Out[53]:
C    0.199283
D    0.119786
Name: 2019-05-29 00:00:00, dtype: float64
In [55]:
df[ df>0.5 ]
Out[55]:
A B C D
2019-05-27 0.632271 NaN NaN NaN
2019-05-28 0.691208 0.700231 0.730246 NaN
2019-05-29 0.603331 NaN NaN NaN
2019-05-30 NaN NaN NaN NaN
2019-05-31 0.552101 NaN 0.702799 NaN
2019-06-01 NaN NaN 0.868320 0.510706
2019-06-02 0.841736 NaN 0.931434 NaN

Setting values

In [61]:
s = pd.Series( np.random.rand(7), index=dates )
s
Out[61]:
2019-05-27    0.547899
2019-05-28    0.465972
2019-05-29    0.127552
2019-05-30    0.996297
2019-05-31    0.691513
2019-06-01    0.029567
2019-06-02    0.376882
Freq: D, dtype: float64
In [63]:
df['E'] = s
df
Out[63]:
A B C D E
2019-05-27 0.632271 0.218192 0.139538 0.082094 0.547899
2019-05-28 0.691208 0.700231 0.730246 0.328330 0.465972
2019-05-29 0.603331 0.165942 0.199283 0.119786 0.127552
2019-05-30 0.043723 0.162669 0.291625 0.120803 0.996297
2019-05-31 0.552101 0.102359 0.702799 0.455912 0.691513
2019-06-01 0.330455 0.227942 0.868320 0.510706 0.029567
2019-06-02 0.841736 0.088304 0.931434 0.300959 0.376882
In [64]:
df.loc[:,['C']] = 0
df
Out[64]:
A B C D E
2019-05-27 0.632271 0.218192 0.0 0.082094 0.547899
2019-05-28 0.691208 0.700231 0.0 0.328330 0.465972
2019-05-29 0.603331 0.165942 0.0 0.119786 0.127552
2019-05-30 0.043723 0.162669 0.0 0.120803 0.996297
2019-05-31 0.552101 0.102359 0.0 0.455912 0.691513
2019-06-01 0.330455 0.227942 0.0 0.510706 0.029567
2019-06-02 0.841736 0.088304 0.0 0.300959 0.376882

Operations

In [68]:
df.mean()
Out[68]:
A    0.527832
B    0.237948
C    0.000000
D    0.274084
E    0.462240
dtype: float64
In [69]:
df.mean(axis=1)
Out[69]:
2019-05-27    0.296091
2019-05-28    0.437148
2019-05-29    0.203322
2019-05-30    0.264698
2019-05-31    0.360377
2019-06-01    0.219734
2019-06-02    0.321576
Freq: D, dtype: float64

Merging dataframes

In [76]:
df1 = pd.DataFrame( np.random.rand(7,2), index=dates, columns=['A','B'])
df2 = pd.DataFrame( np.random.rand(7,3), index=dates, columns=['C','D','E'])
pd.concat([df1,df2],sort=False)
Out[76]:
A B C D E
2019-05-27 0.012169 0.252402 NaN NaN NaN
2019-05-28 0.420066 0.163832 NaN NaN NaN
2019-05-29 0.709032 0.134392 NaN NaN NaN
2019-05-30 0.245606 0.952309 NaN NaN NaN
2019-05-31 0.750060 0.851338 NaN NaN NaN
2019-06-01 0.334091 0.825410 NaN NaN NaN
2019-06-02 0.222300 0.897779 NaN NaN NaN
2019-05-27 NaN NaN 0.781323 0.624619 0.382809
2019-05-28 NaN NaN 0.932316 0.051429 0.823951
2019-05-29 NaN NaN 0.246817 0.021852 0.699723
2019-05-30 NaN NaN 0.700137 0.231148 0.373396
2019-05-31 NaN NaN 0.340692 0.371376 0.751349
2019-06-01 NaN NaN 0.567121 0.771248 0.712765
2019-06-02 NaN NaN 0.970691 0.146501 0.218353
In [78]:
pd.concat([df1,df2],axis=1,join='inner')
Out[78]:
A B C D E
2019-05-27 0.012169 0.252402 0.781323 0.624619 0.382809
2019-05-28 0.420066 0.163832 0.932316 0.051429 0.823951
2019-05-29 0.709032 0.134392 0.246817 0.021852 0.699723
2019-05-30 0.245606 0.952309 0.700137 0.231148 0.373396
2019-05-31 0.750060 0.851338 0.340692 0.371376 0.751349
2019-06-01 0.334091 0.825410 0.567121 0.771248 0.712765
2019-06-02 0.222300 0.897779 0.970691 0.146501 0.218353

Grouping

In [81]:
s = pd.Series( ["a","b","a","c","a","c","b"], index=dates)
df['E']=s
df
Out[81]:
A B C D E
2019-05-27 0.632271 0.218192 0.0 0.082094 a
2019-05-28 0.691208 0.700231 0.0 0.328330 b
2019-05-29 0.603331 0.165942 0.0 0.119786 a
2019-05-30 0.043723 0.162669 0.0 0.120803 c
2019-05-31 0.552101 0.102359 0.0 0.455912 a
2019-06-01 0.330455 0.227942 0.0 0.510706 c
2019-06-02 0.841736 0.088304 0.0 0.300959 b
In [82]:
df.groupby('E').sum()
Out[82]:
A B C D
E
a 1.787704 0.486493 0.0 0.657791
b 1.532944 0.788535 0.0 0.629290
c 0.374178 0.390611 0.0 0.631508

Pivot table

In [105]:
dates = pd.date_range('20190527',periods=6, name='date')
df = pd.DataFrame( np.random.rand(6,3), index=dates, columns=['A','B','C'])
df['D'] = pd.Series(["a","a","b","b","c","c"],index=dates)
df['E'] = pd.Series(["one","two","one","two","one","two"],index=dates)
df
Out[105]:
A B C D E
date
2019-05-27 0.474915 0.196110 0.301641 a one
2019-05-28 0.057920 0.349846 0.670458 a two
2019-05-29 0.878578 0.884794 0.904183 b one
2019-05-30 0.456244 0.917951 0.879430 b two
2019-05-31 0.592064 0.925768 0.601040 c one
2019-06-01 0.403849 0.445142 0.004900 c two
In [106]:
pd.pivot_table(df, values=['A','B','C'], index=['D','E'])
Out[106]:
A B C
D E
a one 0.474915 0.196110 0.301641
two 0.057920 0.349846 0.670458
b one 0.878578 0.884794 0.904183
two 0.456244 0.917951 0.879430
c one 0.592064 0.925768 0.601040
two 0.403849 0.445142 0.004900

Plotting data

In [107]:
%matplotlib inline
df.plot()
Out[107]:
<matplotlib.axes._subplots.AxesSubplot at 0x7f08ba132a20>