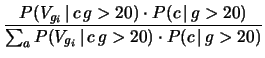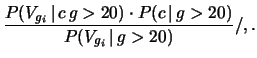Next: Problemi
Up: Previsioni dei risultati
Previous: pzd100Le distribuzioni osservate ``erano''
Indice
L'importanza di aver introdotto il processo di Bernoulli
consiste nell'aver potuto ricondurre molte distribuzioni
di probabilità (geometrica, binomiale, Erlang) ad un solo
processo elementare. La probabilità di eventi complicati
sono quindi calcolati dalla probabilità di eventi semplici,
applicando le regole generali della probabilità. Non sempre è
possibile arrivare a formule compatte per calcolare
la probabilità degli eventi di interesse. Si ricorre
allora a simulazioni di processi elementari che compongono
l'evento complicato. Questi metodi di simulazione sono chiamati
di ``Monte Carlo'', in quanto fanno uso di estrazioni casuali
di numeri, un po' come avviene in un casinò.
Come esempio di un semplice problema impossibile
analiticamente, si pensi al
Gioco dell'Oca.7.4
Per esempio, si
può essere interessati al numero di giri necessari
per vincere. Oppure, si immagini di entrare in una stanza dove
alcuni bambini stanno giocando al gioco dell'oca.
Quanto vale la probabilità che la pedina di un certo
bambino che abbia passato il suo turno
si trovi in una delle caselle numerate da 1 a 62 (a 63 si vince).
Pur essendo l'applicazione banale, la tecnica di simulazione
è concettualmente simile a quella applicata in problemi
di fisica nucleare o di traffico urbano.
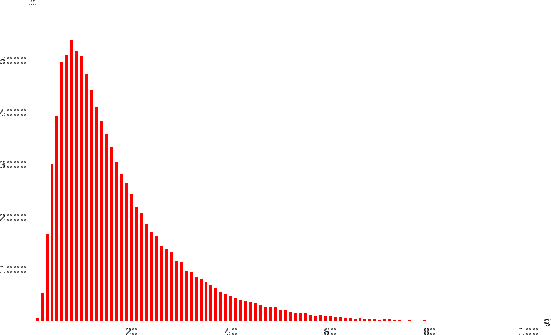
La figura 7.2 mostra la distribuzione di frequenze
dei giri necessari per vincere ottenuta in
10 000 simulazioni. Si noti la lunga coda, dovuta alla regola
di indietreggiare, soprattutto in prossimità dell'arrivo,
qualora si ottenga un punteggio più alto di quello
esattamente necessario per vincere.
000 simulazioni. Si noti la lunga coda, dovuta alla regola
di indietreggiare, soprattutto in prossimità dell'arrivo,
qualora si ottenga un punteggio più alto di quello
esattamente necessario per vincere.
Figura:
Risultato della simulazione di
10 000 volte del gioco dell'oca condotto da una sola persona:
distribuzione del numero
000 volte del gioco dell'oca condotto da una sola persona:
distribuzione del numero  di giri (
di giri ( ) necessari per vincere.
Il diagramma a barre è troncato a
) necessari per vincere.
Il diagramma a barre è troncato a 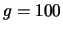 (5 partite superano
tale limite).
(5 partite superano
tale limite).
 |
Come al solito, le code sono meglio apprezzate su scala logaritmica
(figura 7.3).
Figura:
Come figura 7.2,
con la frequenza in scala logaritmica.
 |
Oltre 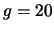 la coda esibisce un andamento esponenziale negativo,
ovvero
la coda esibisce un andamento esponenziale negativo,
ovvero
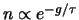 , ove
, ove 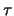 è la ``costante
di tempo'' e vale 12.75.
Quindi, un singolo giocatore può
trascorrere, con probabilità ``zero'', un tempo
``infinito'' per arrivare a vincere.
Infine, la figura 7.4 mostra
la frazione del tempo di occupazione
delle diverse caselle una volta che il giocatore abbia passato la mano.
è la ``costante
di tempo'' e vale 12.75.
Quindi, un singolo giocatore può
trascorrere, con probabilità ``zero'', un tempo
``infinito'' per arrivare a vincere.
Infine, la figura 7.4 mostra
la frazione del tempo di occupazione
delle diverse caselle una volta che il giocatore abbia passato la mano.
Figura:
Frequenza di occupazione delle varie caselle del
gioco dell'oca.
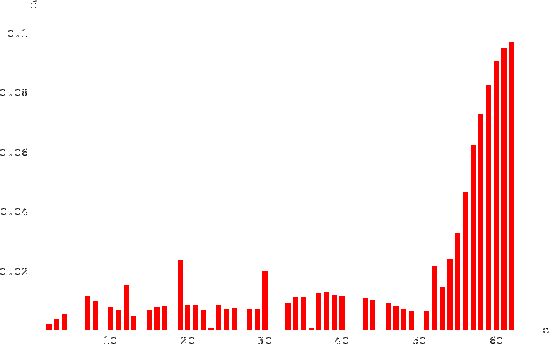 |
Come è noto dall'esperienza, la maggior parte del tempo viene
perso nei rimbalzi intorno alla casella finale, finché essa
non viene centrata esattamente. Si notano gli zeri in corrispondenza
delle caselle da cui si deve avanzare o retrocedere e i picchi
in corrispondenza alle soste forzate o agli avanzamenti/retrocessioni
dirette.
Cerchiamo di capire meglio l'andamento esponenziale della coda.
Esso è dovuto, infatti, ad una distribuzione geometrica
di probabilità, in quanto la probabilità di successo è pari
alla probabilità si insuccesso nei tentativi precedenti
per la probabilità di singolo successo. Chiamando con 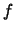 la probabilità
di successo al tentativo
la probabilità
di successo al tentativo  , abbiamo, per
, abbiamo, per 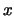 grande (
grande (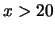 )
)
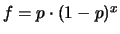 . Riscrivendo opportunamente questa formula otteniamo:
. Riscrivendo opportunamente questa formula otteniamo:
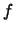 |
 |
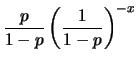 |
(7.13) |
| |
 |
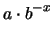 |
(7.14) |
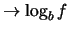 |
 |
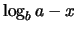 |
(7.15) |
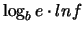 |
 |
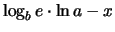 |
(7.16) |
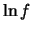 |
 |
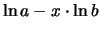 |
(7.17) |
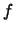 |
 |
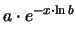 |
(7.18) |
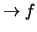 |
 |
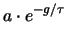 |
(7.19) |
ove 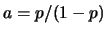 e
e 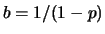 , con
, con 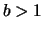 (il caso
(il caso 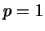 non è preso in considerezione, in quanto poco interessante).
Nell'ultimo passaggio abbiamo chiamato
non è preso in considerezione, in quanto poco interessante).
Nell'ultimo passaggio abbiamo chiamato 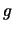 (``giro'')
la generica
(``giro'')
la generica 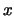 e
e
 . Dal valore di
. Dal valore di
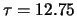 ottenuto dalla simulazione
otteniamo
ottenuto dalla simulazione
otteniamo
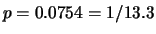 .
.
È interessante confrontare questa probabilità con quella
che si ricava dalla probabilità di occupazione delle varie caselle
e la probabilità di vincere condizionata da ciascuna casella.
Applicando le regole della probabilità abbiamo, indicando con 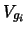 la vittoria ad un generico giro:
la vittoria ad un generico giro:
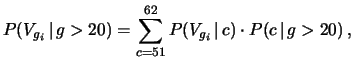 |
(7.20) |
ove
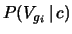 è pari alla probabilità di ottenere
con i due dati il punteggio esatto per vincere (ovvero
è pari alla probabilità di ottenere
con i due dati il punteggio esatto per vincere (ovvero 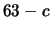 ).
La tabella 7.7 riporta i dettagli del calcolo.
).
La tabella 7.7 riporta i dettagli del calcolo.
Tabella 7.7:
Dettagli del calcolo della probabilità di vincere
al gioco dell'oca, se si sa che il giocatore ha effettuato oltre
20 ``mosse''.
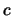 |
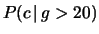 |
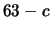 |
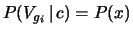 |
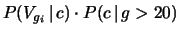 |
| |
(%) |
|
|
(%) |
| |
|
|
|
|
| 51 |
1.0 |
12 |
1/36 |
0.03 |
| 52 |
3.4 |
11 |
2/36 |
0.19 |
| 53 |
2.3 |
10 |
3/36 |
0.19 |
| 54 |
3.7 |
9 |
4/36 |
0.41 |
| 55 |
5.1 |
8 |
5/36 |
0.70 |
| 56 |
7.2 |
7 |
6/36 |
1.20 |
| 57 |
9.7 |
6 |
5/36 |
1.34 |
| 58 |
11.3 |
5 |
4/36 |
1.25 |
| 59 |
12.8 |
4 |
3/36 |
1.06 |
| 60 |
14.0 |
3 |
2/36 |
0.78 |
| 61 |
14.7 |
2 |
1/36 |
0.41 |
| 62 |
15.0 |
1 |
0 |
0 |
| |
|
|
|
|
| |
100.0 |
|
1 |
7.56 |
|
Abbiamo quindi
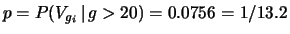 , in perfetto
accordo con quanto calcolato dalla costante di tempo della
coda esponenziale.
, in perfetto
accordo con quanto calcolato dalla costante di tempo della
coda esponenziale.
Come ultimo esercizio su questa simulazione, poniamoci
la seguente domanda. Avendo saputo che una persona ha vinto dopo
molti giri ( ), qual'era la sua posizione prima dell'ultimo
lancvio di dadi?
Si tratta di una semplice applicazione del teorema di Bayes:
), qual'era la sua posizione prima dell'ultimo
lancvio di dadi?
Si tratta di una semplice applicazione del teorema di Bayes:
I valori di probabilità, per le caselle da 51 a 62 sono, in percentuale:
0.4, 2.5, 2.5, 5.4, 9.3, 15.9, 17.7, 16.5, 14.0, 10.3, 5.4, 0.
Sebbene la probabilità di vincere sia massima se ci si trova
nella casella 56, sapere che un bambino ha vinto ci fa pensare
che, con massima probabilità, si trovasse nella casella 57.
Similmente, benché la probabilità di vincere dalle caselle 51
e 61 era la stessa, una volta che il bambino ha vinto ci fa credere
che si trovasse nella casella 61 molto
più probabilmente che nella casella 51.




Next: Problemi
Up: Previsioni dei risultati
Previous: pzd100Le distribuzioni osservate ``erano''
Indice
Giulio D'Agostini
2001-04-02
![]() 000 simulazioni. Si noti la lunga coda, dovuta alla regola
di indietreggiare, soprattutto in prossimità dell'arrivo,
qualora si ottenga un punteggio più alto di quello
esattamente necessario per vincere.
000 simulazioni. Si noti la lunga coda, dovuta alla regola
di indietreggiare, soprattutto in prossimità dell'arrivo,
qualora si ottenga un punteggio più alto di quello
esattamente necessario per vincere.

![]() la probabilità
di successo al tentativo
la probabilità
di successo al tentativo ![]() , abbiamo, per
, abbiamo, per ![]() grande (
grande (![]() )
)
![]() . Riscrivendo opportunamente questa formula otteniamo:
. Riscrivendo opportunamente questa formula otteniamo:
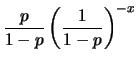
![]() la vittoria ad un generico giro:
la vittoria ad un generico giro:
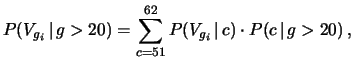
![]() ), qual'era la sua posizione prima dell'ultimo
lancvio di dadi?
Si tratta di una semplice applicazione del teorema di Bayes:
), qual'era la sua posizione prima dell'ultimo
lancvio di dadi?
Si tratta di una semplice applicazione del teorema di Bayes: