



Next: Pallinometro a molte file
Up: Pallinometro e distribuzione binomiale
Previous: Pallinometro e distribuzione binomiale
Indice
Indicando ``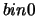 '', ``
'', ``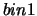 '' e ``
'' e ``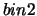 '' i tre possibili
esiti (``bin'' significa, ricordiamo, casella o celletta),
essi non sono da ritenersi equiprobabili. Equiprobabili sono invece,
per ragioni di simmetria, le quattro possibili traiettorie
della pallina.
Assegnamo quindi a ciascuna traiettoria
probabilità 1/4. Poiché due traiettorie terminano in
'' i tre possibili
esiti (``bin'' significa, ricordiamo, casella o celletta),
essi non sono da ritenersi equiprobabili. Equiprobabili sono invece,
per ragioni di simmetria, le quattro possibili traiettorie
della pallina.
Assegnamo quindi a ciascuna traiettoria
probabilità 1/4. Poiché due traiettorie terminano in 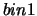 ,
mentre le rimanenti terminano ciascuna in ciascuna delle cellette
adiacenti, otteniamo:
,
mentre le rimanenti terminano ciascuna in ciascuna delle cellette
adiacenti, otteniamo:
Un altro modo per risolvere il problema, formalmente
un po' diverso ma sostanzialmente identico (in quanto fa uso
delle stesse considerazioni di simmetria del problema),
è di fare uso della probabilità condizionata.
Chiamando 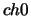 il chiodo fra
il chiodo fra 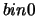 e
e 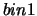 , e
, e 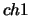 il chiodo fra
il chiodo fra
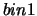 e
e 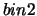 e assegnando probabilità 1/2 a ciascuna delle due
possibilità che ha la pallina per continuare la sua discesa
dopo essere rimbalzata su un chiodo,
otteniamo:
e assegnando probabilità 1/2 a ciascuna delle due
possibilità che ha la pallina per continuare la sua discesa
dopo essere rimbalzata su un chiodo,
otteniamo:
Avendo assegnato queste probabilità, immaginiamo di
voler lanciare  palline (o di lanciare
palline (o di lanciare  volte la stessa pallina)
e di essere interessati al numero di palline che terminano
in ciascuna celletta. Chiamiamo questi numeri
incerti (o variabili casuali)
volte la stessa pallina)
e di essere interessati al numero di palline che terminano
in ciascuna celletta. Chiamiamo questi numeri
incerti (o variabili casuali) 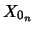 ,
, 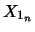 e
e 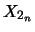 . Date le condizioni, i gradi di fiducia
dei possibili risultati sono descritti da una distribuzione
binomiale di parametri
. Date le condizioni, i gradi di fiducia
dei possibili risultati sono descritti da una distribuzione
binomiale di parametri  e
e 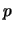 , ove
, ove
 è uguale al numero dei lanci e
è uguale al numero dei lanci e 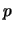 a,
rispettivamente,
a,
rispettivamente, 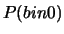 ,
, 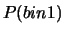 e
e 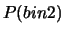 nei tre casi.
Usando il simbolo
nei tre casi.
Usando il simbolo 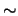 per ``segue la distribuzione'' o, meglio,
``è descritta dalla distribuzione'',7.1 scriviamo
per ``segue la distribuzione'' o, meglio,
``è descritta dalla distribuzione'',7.1 scriviamo
Le probabilità sono date in tabella 7.1
insieme ai valori attesi e alle deviazioni standard.
Tabella:
Distribuzione di probabilità del numero
di palline che terminano in una certa celletta del pallinometro
se si effettuano  lanci.
lanci. 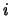 rappresenta l'indice della celletta
di raccolta delle palline
(0 e 2 sone le laterali e 1 la centrale).
I valori più probabili sono
indicati in grassetto.
rappresenta l'indice della celletta
di raccolta delle palline
(0 e 2 sone le laterali e 1 la centrale).
I valori più probabili sono
indicati in grassetto.
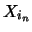 |
 |
 |
| |
|
|
|
|
| |
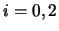 |
 |
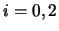 |
 |
| |
|
|
|
|
| 0 |
0.0563 |
0.0010 |
0.0002 |
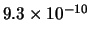 |
| 1 |
0.1877 |
0.0098 |
0.0018 |
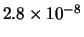 |
| 2 |
0.2816 |
0.0439 |
0.0086 |
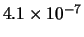 |
| 3 |
0.2503 |
0.1172 |
0.0269 |
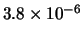 |
| 4 |
0.1460 |
0.2051 |
0.0604 |
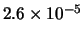 |
| 5 |
0.0584 |
0.2461 |
0.1047 |
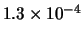 |
| 6 |
0.0162 |
0.2051 |
0.1455 |
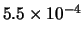 |
| 7 |
0.0031 |
0.1172 |
0.1662 |
0.0019 |
| 8 |
0.0004 |
0.0439 |
0.1593 |
0.0055 |
| 9 |
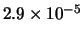 |
0.0098 |
0.1298 |
0.0133 |
| 10 |
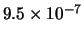 |
0.0010 |
0.0909 |
0.0280 |
| 11 |
0 |
0 |
0.0551 |
0.0509 |
| 12 |
0 |
0 |
0.0291 |
0.0806 |
| 13 |
0 |
0 |
0.0134 |
0.1115 |
| 14 |
0 |
0 |
0.0054 |
0.1354 |
| 15 |
0 |
0 |
0.0019 |
0.1445 |
| 16 |
0 |
0 |
0.0006 |
0.1354 |
| 17 |
0 |
0 |
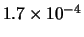 |
0.1115 |
| 18 |
0 |
0 |
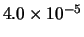 |
0.0806 |
| 19 |
0 |
0 |
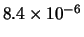 |
0.0509 |
| 20 |
0 |
0 |
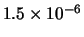 |
0.0280 |
| 21 |
0 |
0 |
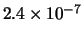 |
0.0133 |
| 22 |
0 |
0 |
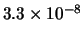 |
0.0055 |
| 23 |
0 |
0 |
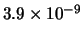 |
0.0019 |
| 24 |
0 |
0 |
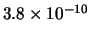 |
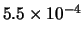 |
| 25 |
0 |
0 |
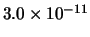 |
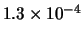 |
| 26 |
0 |
0 |
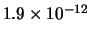 |
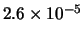 |
| 27 |
0 |
0 |
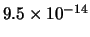 |
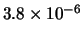 |
| 28 |
0 |
0 |
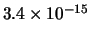 |
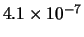 |
| 29 |
0 |
0 |
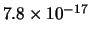 |
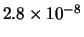 |
| 30 |
0 |
0 |
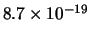 |
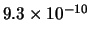 |
| |
|
|
|
|
| |
|
|
|
|
E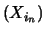 |
2.5 |
5 |
7.5 |
15 |
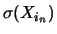 |
1.37 |
1.58 |
2.37 |
2.74 |
| |
|
|
|
|
|




Next: Pallinometro a molte file
Up: Pallinometro e distribuzione binomiale
Previous: Pallinometro e distribuzione binomiale
Indice
Giulio D'Agostini
2001-04-02
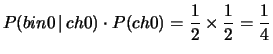
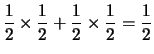
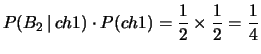
![]() palline (o di lanciare
palline (o di lanciare ![]() volte la stessa pallina)
e di essere interessati al numero di palline che terminano
in ciascuna celletta. Chiamiamo questi numeri
incerti (o variabili casuali)
volte la stessa pallina)
e di essere interessati al numero di palline che terminano
in ciascuna celletta. Chiamiamo questi numeri
incerti (o variabili casuali) ![]() ,
, ![]() e
e ![]() . Date le condizioni, i gradi di fiducia
dei possibili risultati sono descritti da una distribuzione
binomiale di parametri
. Date le condizioni, i gradi di fiducia
dei possibili risultati sono descritti da una distribuzione
binomiale di parametri ![]() e
e ![]() , ove
, ove
![]() è uguale al numero dei lanci e
è uguale al numero dei lanci e ![]() a,
rispettivamente,
a,
rispettivamente, ![]() ,
, ![]() e
e ![]() nei tre casi.
Usando il simbolo
nei tre casi.
Usando il simbolo ![]() per ``segue la distribuzione'' o, meglio,
``è descritta dalla distribuzione'',7.1 scriviamo
per ``segue la distribuzione'' o, meglio,
``è descritta dalla distribuzione'',7.1 scriviamo