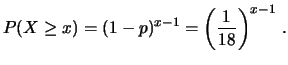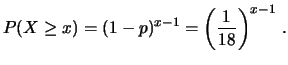Next: Previsioni basate sul teorema
Up: Previsioni dei risultati
Previous: Contatore e distribuzione geometrica
Indice
Consideriamo ora un generico numero al
lotto. Essendo 90 i numeri
in una ruota ed essendone estratti 5, l'ipotesi di equiprobabilità
ci fa valutare in 1/18 la probabilità che un numero venga estratto.
Poiché ogni estrazione avviene indipendentemente dalle altre
e con lo stesso stato di informazione circa i numeri che
possono essere estratti, possiamo considerare ogni estrazione
un processo di Bernoulli avente 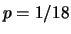 . Analogalmente a
quanto visto per i conteggi, il numero aleatorio
. Analogalmente a
quanto visto per i conteggi, il numero aleatorio 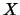 ``estrazione
alla quale uscirà un certo numero predesignato'' (numero e ruota)
è descritto da una distribuzione geometrica di
``estrazione
alla quale uscirà un certo numero predesignato'' (numero e ruota)
è descritto da una distribuzione geometrica di 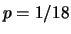 ,
avente previsione e incertezza di previsione
rispettivamente uguali a 18 e 17.5.
Ci possiamo calcolare quindi la probabilità che tale numero
si verifichi all'estrazione
,
avente previsione e incertezza di previsione
rispettivamente uguali a 18 e 17.5.
Ci possiamo calcolare quindi la probabilità che tale numero
si verifichi all'estrazione  , o successiva:
Calcoliamo la probabilità per alcuni valori di
, o successiva:
Calcoliamo la probabilità per alcuni valori di  molto maggiori
della previsione, introducendo inoltre la variabile
molto maggiori
della previsione, introducendo inoltre la variabile 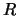 ``numero di
ritardi prima dell'estrazione'':
``numero di
ritardi prima dell'estrazione'':
Essendo il gioco del lotto italiano attivo
da moltissimi anni (ovvero un numero
di estrazioni alcuni ordini di grandezza maggiore di 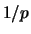 )
la probabilità che un numero qualsiasi abbia, ad un certo istante,
il ritardo
)
la probabilità che un numero qualsiasi abbia, ad un certo istante,
il ritardo 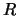 è uguale alla probabilità di
è uguale alla probabilità di 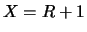 .
Avendo il sistema del lotto italiano 900 numeri in totale
(10 ruote
.
Avendo il sistema del lotto italiano 900 numeri in totale
(10 ruote  90 numeri/ruota)
possiamo calcolare dalla distribuzione
binomiale quanti numeri prevediamo abbiano accumulato
almeno un certo ritardo
90 numeri/ruota)
possiamo calcolare dalla distribuzione
binomiale quanti numeri prevediamo abbiano accumulato
almeno un certo ritardo  . Otteniamo, per i ritardi già
presi in considerazione:
. Otteniamo, per i ritardi già
presi in considerazione:
Come si vede, è molto probabile che, ad un certo istante,
ci sia qualche numero che abbia accumulato
un notevole ritardo. La tabella
1.6 permette di confrontare previsioni e
risultati.
Come al solito, il confronto è confortante, in quanto,
ripetiamo ancora una volta, sarebbe stato alquanto improbabile
osservare una situazione molto lontana dalle aspettative.
In particolare, 27 numeri ritardano da almeno 60 estrazioni,
6 da almeno 80, 3 da almeno 100, 2 da almeno 120 e 1 da almeno 140.




Next: Previsioni basate sul teorema
Up: Previsioni dei risultati
Previous: Contatore e distribuzione geometrica
Indice
Giulio D'Agostini
2001-04-02