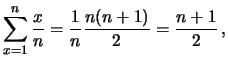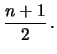Next: Processo di Bernoulli
Up: Valore atteso di distribuzioni
Previous: Valore atteso di distribuzioni
Indice
Nel caso dei primi  interi positivi
abbiamo:
interi positivi
abbiamo:
in accordo con quanto ci si poteva attendere intuitivamente.
Come già visto
a proposito delle funzioni di probabilità anche
per previsioni ed incertezze
conviene talvolta esplicitare il condizionante del
valore atteso, ovvero il tipo di
distribuzione di
probabilità.
Nel nostro caso potremmo scrivere quindi:
Comunque, come anche già detto a proposito di 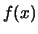 ,
cercheremo di utilizzare semplicemente
E
,
cercheremo di utilizzare semplicemente
E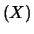 se dal contesto si evince a quale distribuzione ci
si riferisce.
se dal contesto si evince a quale distribuzione ci
si riferisce.
Passiamo ora al caso più generale di distribuzione
uniforme di passo arbitrario:
altro risultato intuitivo.
In entrambi i casi il risultato coincide da quanto ci aspettavamo dal
significato di baricentro della distribuzione e con l'intuizione
che suggerisce che, se una variabile puà assumere
con pari probabilità valori
equidistanziati, questi saranno distribuiti
intorno al centro dell'intervallo.




Next: Processo di Bernoulli
Up: Valore atteso di distribuzioni
Previous: Valore atteso di distribuzioni
Indice
Giulio D'Agostini
2001-04-02