



Next: Binomiale negativa
Up: pzd100 Altre distribuzioni di
Previous: pzd100 Altre distribuzioni di
Indice
Abbiamo studiato la distribuzione geometrica,
legata al numero aleatorio
``tentativo per il quale si registra il primo successo'',
quando si considerano tanti processi di Bernoulli di uguale  .
Il caso più generale è quello che descrive la distribuzione
di probabilità del ``tentativo per il quale si registrano esattamente
.
Il caso più generale è quello che descrive la distribuzione
di probabilità del ``tentativo per il quale si registrano esattamente
 successi''. Essa è nota
come distribuzione di Pascal. La derivazione
è abbastanza semplice:
Essendo i due eventi indipendenti, si ottiene la distribuzione di
probabilità
successi''. Essa è nota
come distribuzione di Pascal. La derivazione
è abbastanza semplice:
Essendo i due eventi indipendenti, si ottiene la distribuzione di
probabilità
Naturalmente, per 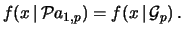 , si riottiene la distribuzione
geometrica, ovvero
, si riottiene la distribuzione
geometrica, ovvero
Figura:
Esempi di distribuzione di Pascal: probabilità
che, lanciando una moneta, si ottengano  , 3 e 5 teste al
tentativo
, 3 e 5 teste al
tentativo  .
.
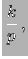 |
Diamo direttamente previsione e incertezza di previsione del
numero aleatorio, descritto da questa distribuzione:
E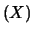 |
 |
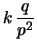 |
(7.11) |
Var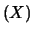 |
 |
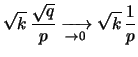 |
(7.12) |
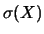 |
 |
![$\displaystyle \sqrt{k}\,\frac{\sqrt{q}}{p}
\xrightarrow[\rightarrow 0]{}\sqrt{k}\,
\frac{1}{p}$](img1472.png) |
(7.13) |
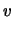 |
 |
![$\displaystyle \frac{1}{\sqrt{k\, q}}\xrightarrow[p\rightarrow 0]{}\frac{1}
{\sqrt{k}}\,.$](img1473.png) |
(7.14) |
Come si capisce intuitivamente,
la previsione del numero
di tentativi per avere  successi è proporzionale
al numero di successi richiesto. Quello che è meno intuitivo, ma
che risulterà
essere una proprietà generale della varianza, è che
non è la deviazione standard, bensì la varianza,
ad essere proporzionale a
successi è proporzionale
al numero di successi richiesto. Quello che è meno intuitivo, ma
che risulterà
essere una proprietà generale della varianza, è che
non è la deviazione standard, bensì la varianza,
ad essere proporzionale a  .
Ne segue che l'incertezza relativa decresce all'aumentare
di
.
Ne segue che l'incertezza relativa decresce all'aumentare
di  .
.




Next: Binomiale negativa
Up: pzd100 Altre distribuzioni di
Previous: pzd100 Altre distribuzioni di
Indice
Giulio D'Agostini
2001-04-02
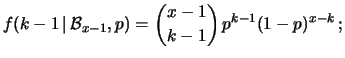 e
e 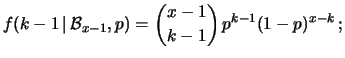 e
e 
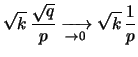
![$\displaystyle \sqrt{k}\,\frac{\sqrt{q}}{p}
\xrightarrow[\rightarrow 0]{}\sqrt{k}\,
\frac{1}{p}$](img1472.png)