



Next: Sufficienza statistica, limite a
Up: Caso generale di inferenza
Previous: pzd100Uso della prior coniugata
Indice
Nei paragrafi precedenti ci siamo concentrati sull'inferenza
di 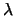 . Il passaggio all'intensità del processo di Poisson
. Il passaggio all'intensità del processo di Poisson  è immediata in quanto
è immediata in quanto  e
e 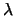 sono legati fra di loro
linearmente
sono legati fra di loro
linearmente
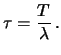 , con
, con 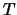 tempo di osservazione
(non si confonda questo
tempo di osservazione
(non si confonda questo  con l'omologo parametro della Gamma).
A volte lo stesso fenomeno modellizzato come un processo
di Poisson è osservato con diversi tempi
di osservazione, ottenemdo
con l'omologo parametro della Gamma).
A volte lo stesso fenomeno modellizzato come un processo
di Poisson è osservato con diversi tempi
di osservazione, ottenemdo 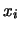 negli intervalli di tempo
negli intervalli di tempo 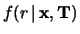 .
Avendo visto ancora una volta l'irrilevanza della esatta forma della
prior nei di interesse pratico e per evitare confusione con il parametro
.
Avendo visto ancora una volta l'irrilevanza della esatta forma della
prior nei di interesse pratico e per evitare confusione con il parametro  della Gamma, usiamo una distribuzione iniziale uniforme.
Ottemiamo, a meno dei soliti fattori moltiplicativi:
della Gamma, usiamo una distribuzione iniziale uniforme.
Ottemiamo, a meno dei soliti fattori moltiplicativi:
e quindi




Next: Sufficienza statistica, limite a
Up: Caso generale di inferenza
Previous: pzd100Uso della prior coniugata
Indice
Giulio D'Agostini
2001-04-02
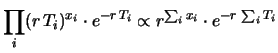
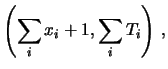
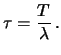 , con
, con 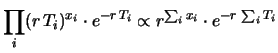
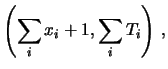
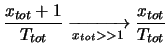
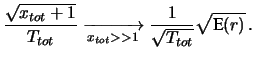
![$\displaystyle \frac{\sqrt{x_{tot}+1}}{T_{tot}}
\xrightarrow[x_{tot}>>1]{} \frac{1}{\sqrt{T_{tot}}}\sqrt{\mbox{E}(r)}\,.$](img3675.png)