 .
.
![]() : 0.417, 0.365, 0.159, 0.046, 0.010, 0.0018.
: 0.417, 0.365, 0.159, 0.046, 0.010, 0.0018.
-
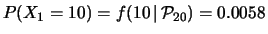 ;
;
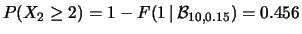
-
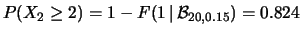 ;
;
 (si noti la dipendenza non lineare da
(si noti la dipendenza non lineare da  : si provi anche
: si provi anche 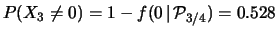 ).
).
-
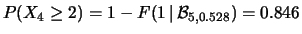 ;
;
-
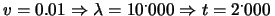 .
.
Affinché
![]() ,
, ![]() (numero medio di molecole nel volumetto)
deve essere pari a 2.3. Ne segue
(numero medio di molecole nel volumetto)
deve essere pari a 2.3. Ne segue
![]() m
m![]() =
=
![]() , ovvero un cubettino
di lato pari a 4.5nm, il quale potrebbe contenere
, ovvero un cubettino
di lato pari a 4.5nm, il quale potrebbe contenere
![]() oggetti di 0.1nm (tipiche dimensioni atomiche).
oggetti di 0.1nm (tipiche dimensioni atomiche).
Per esempio per
![]() :
:
![]() .
.