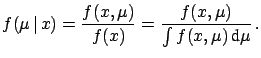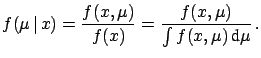Bayes' theorem for uncertain quantities: derivation from a physicist's point of view

Let us show a little more formally the concepts illustrated in the previous section. This is proof of the Bayes' theorem alternative to the proof applied to events, given in Part II of these notes. It is now applied directly to uncertain (i.e. random) quantities, and it should be closer to the physicist's reasoning than the standard proof. For teaching purposes I explain it using time ordering, but this is unnecessary, as explained several times elsewhere.

• Before doing the experiment we are uncertain of the values of $\mu$ and $x$: we know neither the true value, nor the observed value. Generally speaking, this uncertainty is quantified by $f(x, \mu)$.
• Under the hypothesis that we observe $x$, we can calculate the conditional probability
  $$f(\mu\,\vert\, x) = \frac{f(x, \mu)} {f(x)} = \frac{f(x, \mu)} {\int f(x, \mu)\,\mbox{d}\mu}\,.$$

• Usually we don't have $f(x, \mu)$, but this can be calculated by $f(x\,\vert\,\mu)$ and $f(\mu)$:
  $$f(x, \mu) = f(x\,\vert\,\mu)\cdot f(\mu)\,.$$

• If we do an experiment we need to have a good idea of the behaviour of the apparatus; therefore $f(x\,\vert\,\mu)$ must be a narrow distribution, and the most imprecise factor remains the knowledge about $\mu$, quantified by $f(\mu)$, usually very broad. But it is all right that this should be so, because we want to learn about $\mu$.
• Putting all the pieces together we get the standard formula of Bayes' theorem for uncertain quantities:
  $$f(\mu\,\vert\,x) = \frac{f(x\,\vert\,\mu)\cdot f(\mu)} {\int f(x\,\vert\,\mu)\cdot f(\mu)\, \mbox{d}\mu}\,.$$

The steps followed in this proof of the theorem should convince the reader that $f(\mu\,\vert\,x)$ calculated in this way is the best we can say about $\mu$ with the given status of information.