From the probability of the effects to the probability of the causes

The scheme of updating knowledge that we will use is that of Bayesian statistical inference, widely discussed in the second part of this report (in particular Sections and ). I wish to make a less formal presentation of it here, to show that there is nothing mysterious behind Bayes' theorem, and I will try to justify it in a simple way.

Figure: Deduction and induction.

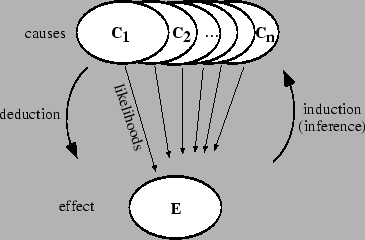
It is very convenient to consider true values and observed values as causes and effects (see Fig. , imagining also a continuous set of causes and many possible effects). The process of going from causes to effects it is called `deduction'.^2.11 The possible values $x$ which may be observed are classified in belief by

$$f(x\,\vert\,\mu)\,.$$

This function is called `likelihood' since it quantifies how likely it is that $\mu$ will produce any given $x$. It summarizes all previous knowledge on that kind of measurement (behaviour of the instruments, of influence factors, etc. - see list in Section ). Often, if one deals only with random error, the $f(x\,\vert\,\mu)$ is a normal distribution around $\mu$, but in principle it may have any form.

Once the likelihood is determined (we have the performance of the detector under control) we can build $f(\mu\,\vert\,x)$, under the hypothesis that $x$ will be observed.^2.12 In order to arrive at the general formula in an heuristic way, let us consider only two values of $\mu$. If they seem to us equally possible, it will seem natural to be in favour of the value which gives the highest likelihood that $x$ will be observed. For example, assuming $\mu_1=-1$, $\mu_2=10$, considering a normal likelihood with $\sigma = 3$, and having observed $x=2$, one tends to believe that the observation is most likely caused by $\mu_1$. If, on the other hand, the quantity of interest is positively defined, then $\mu_1$ switches from most probable to impossible cause; $\mu_2$ becomes certain. There are, in general, intermediate cases in which, because of previous knowledge (see, e.g., Fig. and related text), one tends to believe a priori more in one or other of the causes. It follows that, in the light of a new observation, the degree of belief of a given value of $\mu$ will be proportional to

-

the likelihood that $\mu$ will produce the observed effect;

-

the degree of belief attributed to $\mu$ before the observation, quantified by $f_\circ(\mu)$.

We have finally:

$$f(\mu\,\vert\,x)\propto f(x\,\vert\,\mu)\cdot f_\circ(\mu)\,.$$

This is one of the ways to write Bayes' theorem.