



Next: Conditional probability
Up: Conditional probability and Bayes'
Previous: Conditional probability and Bayes'
Contents
Dependence of the probability on the
state of information
If the state of information changes, the evaluation of
the probability also has to be modified. For example
most people would agree that the probability
of a car being stolen depends on the model, age and parking site.
To take an example from physics, the probability that
in a HERA detector a charged particle
of
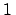 GeV
gives a certain number of ADC counts due
to the energy loss in a gas detector can be evaluated
in a very general way -- using High Energy Physics jargon -- by making a
(huge) Monte Carlo simulation which takes into account all
possible reactions (weighted with their cross-sections),
all possible backgrounds, changing all physical and detector
parameters within reasonable ranges, and also taking into
account the trigger efficiency. The probability
changes if one knows that the particle is a
GeV
gives a certain number of ADC counts due
to the energy loss in a gas detector can be evaluated
in a very general way -- using High Energy Physics jargon -- by making a
(huge) Monte Carlo simulation which takes into account all
possible reactions (weighted with their cross-sections),
all possible backgrounds, changing all physical and detector
parameters within reasonable ranges, and also taking into
account the trigger efficiency. The probability
changes if one knows that the particle is a 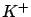 : instead of very
complicated Monte Carlo simulation one can just run a single particle
generator. But then it changes further if one also knows the
exact gas mixture,
pressure, etc., up to the latest
determination of the pedestal and the temperature of the ADC module.
: instead of very
complicated Monte Carlo simulation one can just run a single particle
generator. But then it changes further if one also knows the
exact gas mixture,
pressure, etc., up to the latest
determination of the pedestal and the temperature of the ADC module.




Next: Conditional probability
Up: Conditional probability and Bayes'
Previous: Conditional probability and Bayes'
Contents
Giulio D'Agostini
2003-05-15