



Next: Bayes' theorem
Up: Conditional probability and Bayes'
Previous: Dependence of the probability
Contents
Conditional probability
Although everybody knows the formula of conditional probability,
it is useful to derive it here3.5.
The notation is
 ,
to be read ``probability of
,
to be read ``probability of  given
given  '', where
'', where  stands for
hypothesis.
This means: the probability that
stands for
hypothesis.
This means: the probability that  will occur under the
hypothesis that
will occur under the
hypothesis that  has occurred3.6.
has occurred3.6.
The event 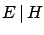 can have three values:
can have three values:
- TRUE:
- if
 is TRUE and
is TRUE and  is TRUE;
is TRUE;
- FALSE:
- if
 is FALSE and
is FALSE and  is TRUE;
is TRUE;
- UNDETERMINED:
- if
 is FALSE; in this case we are merely
uninterested in what happens to
is FALSE; in this case we are merely
uninterested in what happens to  . In terms
of betting, the bet is
invalidated and none loses or gains.
. In terms
of betting, the bet is
invalidated and none loses or gains.
Then 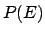 can be written
can be written
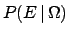 ,
to state explicitly that it is the probability of
,
to state explicitly that it is the probability of
 whatever happens to the rest of the world
(
whatever happens to the rest of the world
(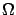 means all possible events). We realize immediately
that this condition is really too vague and nobody would
bet a penny on a such a statement. The reason for usually
writing
means all possible events). We realize immediately
that this condition is really too vague and nobody would
bet a penny on a such a statement. The reason for usually
writing 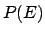 is that many conditions
are implicitly, and reasonably, assumed in most
circumstances. In the classical problems of coins and dice, for example,
one assumes that they are regular. In the example
of the energy loss,
it was implicit (``obvious'') that the
high voltage was on (at which voltage?)
and that HERA was running (under which condition?).
But one has to take care: many riddles are
based on the fact that one tries to find a solution which is
valid under more strict conditions than those explicitly stated
in the question, and many people make bad business deals by signing
contracts in which what ``was obvious''
was not explicitly stated.
is that many conditions
are implicitly, and reasonably, assumed in most
circumstances. In the classical problems of coins and dice, for example,
one assumes that they are regular. In the example
of the energy loss,
it was implicit (``obvious'') that the
high voltage was on (at which voltage?)
and that HERA was running (under which condition?).
But one has to take care: many riddles are
based on the fact that one tries to find a solution which is
valid under more strict conditions than those explicitly stated
in the question, and many people make bad business deals by signing
contracts in which what ``was obvious''
was not explicitly stated.
In order to derive the formula of conditional probability
let us assume for a moment that it is reasonable to
talk about
``absolute probability''
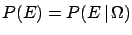 ,
and let us rewrite
,
and let us rewrite
where the result has been achieved through the following steps:
- (a)
 implies
implies 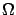 (i.e.
(i.e.
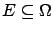 )
and hence
)
and hence
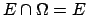 ;
;
- (b)
- the complementary events
 and
and
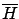 make a finite partition of
make a finite partition of 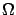 ,
i.e.
,
i.e.
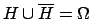 ;
;
- (c)
- distributive property;
- (d)
- axiom 3.
The final result of (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) is very simple:
) is very simple:
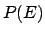 is equal to the probability that
is equal to the probability that  occurs and
occurs and  also
occurs, plus the probability that
also
occurs, plus the probability that  occurs but
occurs but  does not
occur. To obtain
does not
occur. To obtain
 we just get rid of the subset of
we just get rid of the subset of
 which does not contain
which does not contain  (i.e.
(i.e.
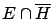 )
and renormalize the probability
dividing by
)
and renormalize the probability
dividing by 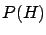 , assumed to be different from zero. This guarantees
that if
, assumed to be different from zero. This guarantees
that if 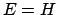 then
then
 .
We get, finally, the well known formula
.
We get, finally, the well known formula
![$\displaystyle P(E\,\vert\,H) = \frac{P(E\cap H)}{P(H)}\hspace{1.0cm}[P(H)\ne 0]\,.$](img285.png) |
(3.2) |
In the most general (and realistic)
case, where both  and
and  are conditioned by the occurrence of
a third event
are conditioned by the occurrence of
a third event 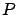 , the formula becomes
, the formula becomes
![$\displaystyle P(E\,\vert\,H, H_\circ) = \frac{P\left[E\cap (H\,\vert\, H_\circ]\right) } {P(H\,\vert\,H_\circ)}\hspace{1.0cm}[P(H\,\vert\,H_\circ)\ne 0]\,.$](img286.png) |
(3.3) |
Usually we shall make use of (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
(which means
)
(which means
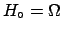 ) assuming that
) assuming that 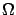 has been
properly chosen.
We should also remember that (
has been
properly chosen.
We should also remember that (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) can be resolved
with respect to
) can be resolved
with respect to
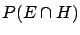 , obtaining the well known
, obtaining the well known
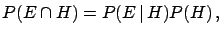 |
(3.4) |
and by symmetry
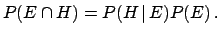 |
(3.5) |
We remind that two events are called independent if
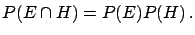 |
(3.6) |
This is equivalent to saying that
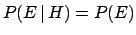 and
and
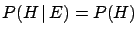 ,
i.e. the knowledge that one event has occurred does not change the
probability of the other. If
,
i.e. the knowledge that one event has occurred does not change the
probability of the other. If
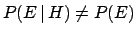 then the events
then the events
 and
and  are correlated. In particular:
are correlated. In particular:
- if
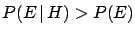 then
then  and
and  are positively correlated;
are positively correlated;
- if
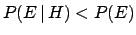 then
then  and
and  are negatively correlated.
are negatively correlated.




Next: Bayes' theorem
Up: Conditional probability and Bayes'
Previous: Dependence of the probability
Contents
Giulio D'Agostini
2003-05-15
![]() can have three values:
can have three values:
![]() ,
and let us rewrite
,
and let us rewrite