



Next: Normal approximation of the
Up: Central limit theorem
Previous: Terms and role
Contents
Distribution of a sample average
As first application of the theorem, let us remind ourselves that
a sample average
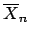 of
of 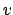 independent variables,
independent variables,
is normally distributed, since it is a linear combination
of 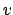 variables
variables 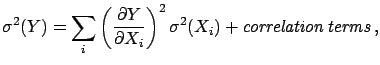 , with
, with 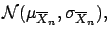 . Then,
. Then,
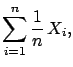 |
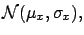 |
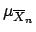 |
(4.75) |
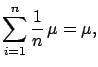 |
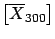 |
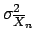 |
(4.76) |
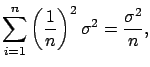 |
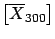 |
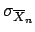 |
(4.77) |
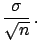 |
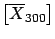 |
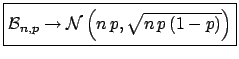 |
(4.78) |
This result, we repeat, is independent of the distribution
of  and is already approximately valid for small values of
and is already approximately valid for small values of 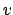 .
.
Giulio D'Agostini
2003-05-15
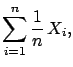
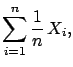
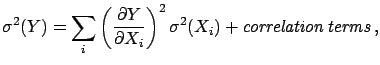 , with
, with 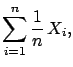
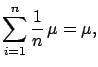
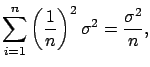
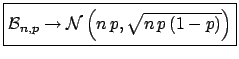
 and is already approximately valid for small values of
and is already approximately valid for small values of