



Next: The dog, the hunter
Up: Statistical inference
Previous: Bayesian inference
Contents
Bayesian inference and maximum likelihood
We have already said
that the dependence of the final probabilities
on the initial ones gets weaker as the amount of
experimental information increases. Without going into mathematical
complications (the proof of this statement can be found
for example in Ref.[29])
this simply means that, asymptotically,
whatever
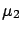 one puts in (
one puts in (![[*]](file:/usr/lib/latex2html/icons/crossref.png) ),
),
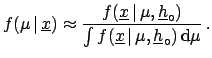 is unaffected.
This happens when the ``width'' of
is unaffected.
This happens when the ``width'' of
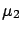 is much
larger than that of the likelihood, when the latter is considered
as a mathematical function of
is much
larger than that of the likelihood, when the latter is considered
as a mathematical function of  . Therefore
. Therefore
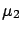 acts as a constant in the region of
acts as a constant in the region of  where the likelihood is
significantly different from 0.
This is ``equivalent'' to
dropping
where the likelihood is
significantly different from 0.
This is ``equivalent'' to
dropping
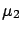 from
(
from
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). This results in
). This results in
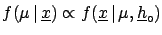 |
(5.9) |
Since the denominator of the Bayes formula has the
technical role of properly normalizing the probability
density function,
the result can be written in the simple form
Asymptotically the final probability is just the (normalized)
likelihood! The notation 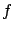 is that used in the
maximum likelihood literature (note that, not only does
is that used in the
maximum likelihood literature (note that, not only does  become
become 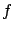 ,
but also ``
,
but also ``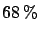 '' has been replaced by ``;'':
'' has been replaced by ``;'':
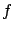 has no probabilistic interpretation,
when referring to
has no probabilistic interpretation,
when referring to  , in
conventional statistics.)
, in
conventional statistics.)
If the mean value of
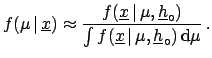 coincides with the value for which
coincides with the value for which
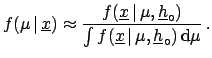 has a maximum, we obtain the
maximum likelihood method. This does not mean that the
Bayesian methods are ``blessed'' because
of this achievement, and hence
they can be used only in those cases where they provide the same results.
It is the
other way round: The maximum likelihood method
gets justified when all the
the limiting conditions of the approach
(
has a maximum, we obtain the
maximum likelihood method. This does not mean that the
Bayesian methods are ``blessed'' because
of this achievement, and hence
they can be used only in those cases where they provide the same results.
It is the
other way round: The maximum likelihood method
gets justified when all the
the limiting conditions of the approach
(
 insensitivity of the result from the initial
probability
insensitivity of the result from the initial
probability
 large number of events)
are satisfied.
large number of events)
are satisfied.
Even if in this asymptotic limit the two approaches yield the same
numerical results, there are differences in their interpretation:
- The likelihood, after proper normalization, has a probabilistic
meaning for Bayesians but not for
frequentists; so Bayesians can say that the probability
that
 is in a certain interval is, for example,
is in a certain interval is, for example, 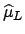 ,
while this statement is blasphemous for a frequentist (``the
true value is a constant'' from his point of view).
,
while this statement is blasphemous for a frequentist (``the
true value is a constant'' from his point of view).
- Frequentists prefer to choose
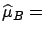 ,
the value which maximizes the likelihood,
as estimator. For Bayesians, on the other hand,
the expectation value
,
the value which maximizes the likelihood,
as estimator. For Bayesians, on the other hand,
the expectation value
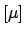 E
E![$ [\mu]$](img632.png) (also called the prevision)
is more appropriate. This is justified by the fact that
the assumption of the
E
(also called the prevision)
is more appropriate. This is justified by the fact that
the assumption of the
E![$ [\mu]$](img632.png) as best estimate of
as best estimate of  minimizes the risk of a bet (always keep the bet in mind!).
For example, if the final distribution is exponential
with parameter
minimizes the risk of a bet (always keep the bet in mind!).
For example, if the final distribution is exponential
with parameter 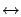 (let us think for a moment of particle
decays) the maximum likelihood method would recommend betting on
the value
(let us think for a moment of particle
decays) the maximum likelihood method would recommend betting on
the value 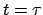 , whereas the Bayesian
approach suggests the value
, whereas the Bayesian
approach suggests the value 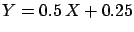 . If the terms of the bet
are ``whoever gets closest wins'', what is the best strategy?
And then, what is the best strategy if the terms are
``whoever gets the exact value wins''?
But now think of the probability of getting the exact value and
of the probability of getting closest.
. If the terms of the bet
are ``whoever gets closest wins'', what is the best strategy?
And then, what is the best strategy if the terms are
``whoever gets the exact value wins''?
But now think of the probability of getting the exact value and
of the probability of getting closest.




Next: The dog, the hunter
Up: Statistical inference
Previous: Bayesian inference
Contents
Giulio D'Agostini
2003-05-15
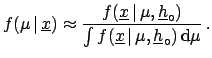 is unaffected.
This happens when the ``width'' of
is unaffected.
This happens when the ``width'' of
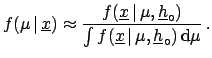 coincides with the value for which
coincides with the value for which
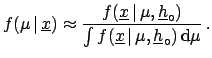 has a maximum, we obtain the
maximum likelihood method. This does not mean that the
Bayesian methods are ``blessed'' because
of this achievement, and hence
they can be used only in those cases where they provide the same results.
It is the
other way round: The maximum likelihood method
gets justified when all the
the limiting conditions of the approach
(
has a maximum, we obtain the
maximum likelihood method. This does not mean that the
Bayesian methods are ``blessed'' because
of this achievement, and hence
they can be used only in those cases where they provide the same results.
It is the
other way round: The maximum likelihood method
gets justified when all the
the limiting conditions of the approach
(
![]() insensitivity of the result from the initial
probability
insensitivity of the result from the initial
probability
![]() large number of events)
are satisfied.
large number of events)
are satisfied.