



Next: Bertrand paradox and angels'
Up: Choice of the initial
Previous: Choice of the initial
Contents
Figure:
Examples of variable changes starting from
a uniform distribution (``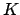 ''):
A)
''):
A)
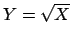 ;
B)
;
B) 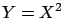 ; C)
; C) 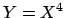 ; D)
; D) 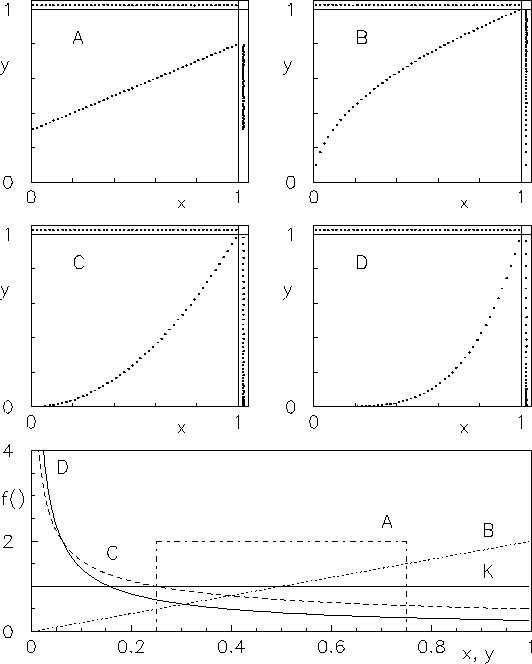 .
.
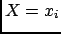 |
The title of this section is similar to that of Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) , but
the problem and the conclusions will be different. There we said that
the Indifference Principle (or, in its refined modern version, the
Maximum Entropy Principle) was a good choice. Here there are problems
with infinities
and with the fact that it is possible to map an infinite
number of points contained in a finite region onto an infinite
number of points contained in a larger or smaller
finite region. This changes the probability density
function. If, moreover, the transformation from one
set of variables to the
other is not linear (see, e.g., Fig.
, but
the problem and the conclusions will be different. There we said that
the Indifference Principle (or, in its refined modern version, the
Maximum Entropy Principle) was a good choice. Here there are problems
with infinities
and with the fact that it is possible to map an infinite
number of points contained in a finite region onto an infinite
number of points contained in a larger or smaller
finite region. This changes the probability density
function. If, moreover, the transformation from one
set of variables to the
other is not linear (see, e.g., Fig. ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ),
what is uniform in one variable (
),
what is uniform in one variable ( )
is not uniform in another variable (e.g.
)
is not uniform in another variable (e.g. 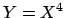 ). This problem
does not exist in the
case of discrete variables, since if
). This problem
does not exist in the
case of discrete variables, since if 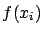 has a probability
has a probability
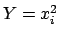 then
then  has the same probability.
A different way of stating the problem is that the
Jacobian of the
transformation squeezes or stretches the metrics, changing the
probability density function.
has the same probability.
A different way of stating the problem is that the
Jacobian of the
transformation squeezes or stretches the metrics, changing the
probability density function.
We will not enter into the open
discussion about the optimal choice
of the distribution. Essentially we shall use the uniform distribution,
being careful to employ the variable which ``seems'' most appropriate
for the problem, but You may disagree
-- surely with good reason -- if You have a different
kind of experiment in mind.
The same problem is also present, but well hidden,
in the maximum likelihood method.
For example, it is possible to demonstrate
that, in the case of normally distributed likelihoods,
a uniform distribution of the mean  is implicitly assumed
(see Section
is implicitly assumed
(see Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
There is nothing wrong with this, but one should be aware
of it.
).
There is nothing wrong with this, but one should be aware
of it.




Next: Bertrand paradox and angels'
Up: Choice of the initial
Previous: Choice of the initial
Contents
Giulio D'Agostini
2003-05-15
 )
is not uniform in another variable (e.g.
)
is not uniform in another variable (e.g. ![]() is implicitly assumed
(see Section
is implicitly assumed
(see Section ![]() ).
There is nothing wrong with this, but one should be aware
of it.
).
There is nothing wrong with this, but one should be aware
of it.